W tym zadaniu musisz wyznaczyć objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy długości a, zaś jego krawędzie boczne leżące naprzeciw stykają się pod kątem α.
![]()
![]()
Krawędź boczna, wysokość oraz połowa przekątnej podstawy tworzą trójkąt prostokątny, w którym kąt między wysokością a krawędzią boczną to połowa kąta między dwiema naprzeciwległymi krawędziami bocznymi.
Połowa przekątnej podstawy: ![]()
Miara kąta: ![]()
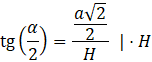
![]()
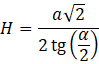
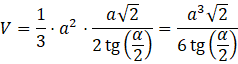

Do obliczenia objętości ostrosłupa potrzebujesz pola powierzchni jego podstawy oraz wysokości. Podstawą w ostrosłupie czworokątnym prawidłowym jest kwadrat, więc jego pole wynosi a2.
Zauważ, że krawędź boczna, wysokość oraz połowa przekątnej podstawy tworzą trójkąt prostokątny, w którym kąt między wysokością a krawędzią boczną to połowa kąta między dwiema naprzeciwległymi krawędziami bocznymi (jest tak, gdyż graniastosłup jest prawidłowy i wszystkie krawędzie boczne są równe). Przekątna podstawy to przekątna kwadratu i korzystając ze wzoru na długość przekątnej kwadratu wynosi ona ![]()
![]()
![]()
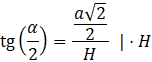
Wyznacz z tego równania wysokość H, przez przemnożenie obu stron przez tę wysokość oraz podzielenie przez tangensa.
![]()
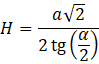
Mając te informacje możesz obliczyć objętość tego ostrosłupa.
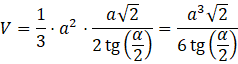

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
