W tym zadaniu trzeba rozwiązać problem dotyczący drutu długości 10 m, który został podzielony na dwie części. Z jednej z nich wykonano kwadratową ramkę, a z drugiej – prostokątną taką, że jeden jej bok ma taką samą długość jak bok kwadratu. Po zsumowaniu powierzchni obszarów ograniczonych tymi ramkami otrzymujemy 3 m2. Należy wyznaczyć wymiary obu ramek.
x – długość boku kwadratowej ramki
4x – obwód kwadratowej ramki, czyli ilość drutu zużyta na nią
x2 – pole powierzchni ograniczonej przez pierwszą ramkę
y – długość boku prostokątnej ramki, która nie ma takiej samej długości jak kwadratowa
2x+2y – obwód prostokątnej ramki, czyli ilość drutu zużyta na nią
xy – pole powierzchni ograniczonej przez drugą ramkę
4x+2x+2y=6x+2=10 m – długość całego drutu
x2 + xy = 3 m2 – łączne pole powierzchni ograniczone przez obie ramki
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
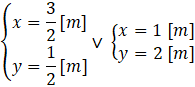
Odp.: Ramki mają wymiary 1,5 m x 1,5 m i 1,5 m x 0,5 m lub 1 m x 1 m i 1 m x 2 m.

W tego typu zadaniach dobrze jest wypisać sobie wszystkie dane. Opisujesz niewiadome i za ich pomocą wyrażasz potrzebne wielkości. Tutaj potrzebujesz długości boków obydwu ramek i wiesz, ile łącznie drutu zużyto. Dlatego przydadzą się tobie informacje na temat obwodów ramek. Wiesz także ile wynosi suma powierzchni ograniczonych przez te ramki, dlatego warto zastanowić się nad powierzchniami tych ramek. Gdy już wypiszesz wszystko co wiesz z treści oraz wszystko co potrzebujesz, możesz przystąpić do rozwiązywania otrzymanych równań. Najpierw wyznaczasz y w zależności od x (można by było zrobić na odwrót, jednakże nie dość, że dostałbyś ułamki, to byś musiał podstawiać to w dwóch miejscach w kolejnym równaniu).
![]()
![]()
![]()
Następnie otrzymane wyrażenie równe y, podstawiasz w odpowiednim miejscu w drugim równaniu.
![]()
![]()
Po uproszczeniu otrzymujesz typowe równanie kwadratowe, które rozwiązujesz przy użyciu Δ.
![]()
![]()
![]()
![]()
![]()
Musisz zwrócić uwagę, czy otrzymane rozwiązania są dodatnie, gdyż długości boku kwadratu nie można wyrazić za pomocą liczb ujemnych. Gdy otrzymasz wartości x, podstaw je do wzoru, na y który wcześniej otrzymałeś.
![]()
![]()
Na sam koniec pamiętaj by w odpowiedzi podać wymiary obydwu ramek w dwóch przypadkach. Nie zapomnij także o jednostkach.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
