W sposób opisany w zadaniu możesz zbudować wielokąt o dowolnej ilości boków. Jednakże nie zawsze na takim wielokącie da się zbudować ostrosłup w sposób opisany w zadaniu. Należy zauważyć, że w każdym ostrosłupie możesz wyróżnić trójkąt prostokątny którego przyprostokątnymi będą wysokość oraz promień okręgu opisanego na podstawie (tylko w przypadku ostrosłupów prawidłowych, które tu się rozważa) zaś przeciwprostokątną będzie krawędź boczna ostrosłupa. W opisywanych ostrosłupach krawędź boczna będzie wynosiła długość zapałki, czyli 4 cm. W trójkącie prostokątnym przeciwprostokątna musi być najdłuższym bokiem, jeśli któraś z „przyprostokątnych” będzie dłuższa od przeciwprostokątnej, wtedy nie da się utworzyć trójkąta prostokątnego. O ile wysokość ostrosłupa nie zależy od figury w podstawie, tak długość promienia okręgu opisanego już tak. Więc ostrosłupa w sposób opisany w treści zadania nie będzie dało się zbudować, jeśli promień okręgu opisanego na podstawie będzie równy lub większy od krawędzi podstawy.
Okazuje się, że dla sześciokąta foremnego promień okręgu opisanego na nim jest dokładnie równy długości boku, co oznacza, że ostrosłupa prawidłowego sześciokątnego nie da się zbudować w sposób opisany w zadaniu. Zwiększanie ilości boków w wielokącie foremnym powoduje zwiększanie się promienia opisanego na wielokącie, więc dla większej ilości boków figury w podstawie tym bardziej nie da się zbudować w sposób opisany w zadaniu ostrosłupa. Pozostaje jedynie się upewnić, czy da się zbudować takie ostrosłupy dla figur o mniejszej niż sześciokąt liczbie boków.
W przypadku podstawy będącej trójkątem równobocznym, promień okręgu opisanego wynosi ![]()
![]()
W przypadku ostrosłupa prawidłowego czworokątnego, promień opisany da podstawie ma długość połowy przekątnej, czyli ![]()
Pozostaje jeszcze ostrosłup o podstawie pięciokąta foremnego. Z wierzchołków pięciokąta do jego środka można poprowadzić odcinki (które to właśnie będą promieniem okręgu opisanego na pięciokącie) i utworzyć w ten sposób pięć trójkątów przystających do siebie (takich samych). Będą to trójkąty równoramienne o podstawie w boku tego pięciokąta. Kąt naprzeciwko podstawy będzie piątą częścią kąta pełnego, czyli jego miara będzie wynosiła 360° : 5 = 72°. Z twierdzenia cosinusów:
![]()
![]()
![]()
![]()
![]()
![]()
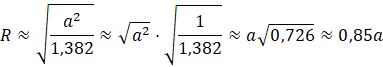
Więc promień okręgu opisanego na pięciokącie jest mniejszy od jego boku, czyli da się w sposób opisany w zadaniu skonstruować ostrosłup prawidłowy.
Podsumowując, w sposób opisany w treści zadania da się zbudować ostrosłup prawidłowy trójkątny, czworokątny oraz pięciokątny.
Przy określonej krawędzi bocznej wysokość ostrosłupa będzie tym mniejsza im większy będzie promień okręgu opisanego na podstawie. Spośród trzech ostrosłupów przedstawionych w zadaniu największy promień okręgu opisanego będzie dla ostrosłupa pięciokątnego i ten ostrosłup będzie najniższy.
![]()
![]()
![]()
![]()
![]()
![]()

W sposób opisany w zadaniu możesz zbudować wielokąt o dowolnej ilości boków. Jednakże nie zawsze na takim wielokącie da się zbudować ostrosłup w sposób opisany w zadaniu. Zauważ, że w każdym ostrosłupie możesz wyróżnić trójkąt prostokątny którego przyprostokątnymi będą wysokość oraz promień okręgu opisanego na podstawie (tylko w przypadku ostrosłupów prawidłowych, które tu się rozważa) zaś przeciwprostokątną będzie krawędź boczna ostrosłupa. W opisywanych ostrosłupach krawędź boczna będzie wynosiła długość zapałki, czyli 4 cm. W trójkącie prostokątnym przeciwprostokątna musi być najdłuższym bokiem, jeśli któraś z „przyprostokątnych” będzie dłuższa od przeciwprostokątnej, wtedy nie da się utworzyć trójkąta prostokątnego. O ile wysokość ostrosłupa nie zależy od figury w podstawie, tak długość promienia okręgu opisanego już tak. Więc ostrosłupa w sposób opisany w treści zadania nie będzie dało się zbudować, jeśli promień okręgu opisanego na podstawie będzie równy lub większy od krawędzi podstawy.
Okazuje się, że dla sześciokąta foremnego promień okręgu opisanego na nim jest dokładnie równy długości boku, co oznacza, że ostrosłupa prawidłowego sześciokątnego nie da się zbudować w sposób opisany w zadaniu. Zwiększanie ilości boków w wielokącie foremnym powoduje zwiększanie się promienia opisanego na wielokącie, więc dla większej ilości boków figury w podstawie tym bardziej nie da się zbudować w sposób opisany w zadaniu ostrosłupa. Pozostaje jedynie się upewnić, czy da się zbudować takie ostrosłupy dla figur o mniejszej niż sześciokąt liczbie boków.
W przypadku podstawy będącej trójkątem równobocznym, promień okręgu opisanego wynosi ![]()
![]()
W przypadku ostrosłupa prawidłowego czworokątnego, promień opisany da podstawie ma długość połowy przekątnej, czyli ![]()
Pozostaje jeszcze ostrosłup o podstawie pięciokąta foremnego. Z wierzchołków pięciokąta do jego środka można poprowadzić odcinki (które to właśnie będą promieniem okręgu opisanego na pięciokącie) i utworzyć w ten sposób pięć trójkątów przystających do siebie (takich samych). Będą to trójkąty równoramienne o podstawie w boku tego pięciokąta. Kąt naprzeciwko podstawy będzie piątą częścią kąta pełnego, czyli jego miara będzie wynosiła 360° : 5 = 72°. Z twierdzenia cosinusów możesz wyznaczyć długość okręgu opisanego na pięciokącie foremnym, w zależności od boku a:
![]()
Wartość cosinusa 72° odczytaj z tablic wartości trygonometrycznych.
![]()
Wyciągnij przed nawias 2R2.
![]()
![]()
![]()
![]()
Oczywiście nie ma sensu rozważać ujemnej wartości promienia oraz ujemnych wartości boku.
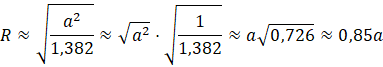
Więc promień okręgu opisanego na pięciokącie jest mniejszy od jego boku, czyli da się w sposób opisany w zadaniu skonstruować ostrosłup prawidłowy.
Podsumowując, w sposób opisany w treści zadania da się zbudować ostrosłup prawidłowy trójkątny, czworokątny oraz pięciokątny.
Przy określonej krawędzi bocznej wysokość ostrosłupa będzie tym mniejsza im większy będzie promień okręgu opisanego na podstawie. Spośród trzech ostrosłupów przedstawionych w zadaniu największy promień okręgu opisanego będzie dla ostrosłupa pięciokątnego i ten ostrosłup będzie najniższy. Jego wysokość możesz obliczyć z twierdzenia Pitagorasa. Oczywiście Najpierw oblicz długość okręgu opisanego na podstawie korzystając z wcześniej wyprowadzonego wzoru:
![]()
![]()
![]()
![]()
![]()
Ponieważ wysokość nie może być ujemna odrzuć od razu ujemny przypadek.
![]()