W tym zadaniu musisz uzasadnić, że dokładniej w tej kolejności liczby ![]()
Aby udowodnić, że podane liczby stanowią ciąg geometryczny wystarczy pokazać, że spełniają własność dotyczącą trzech kolejnych wyrazów ciągu geometrycznego:
![]()
![]()
![]()
![]()
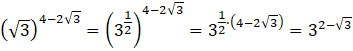
![]()
![]()
Więc podstawione liczby spełniają wyjściową zależność. Oznacza to, że te liczby są kolejnymi elementami ciągu geometrycznego, co należało wykazać.
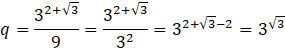
![]()
![]()
![]()
Odp.: Tak, iloraz tego ciągu jest większy od 3.

Aby udowodnić, że podane liczby stanowią ciąg geometryczny wystarczy pokazać, że spełniają własność dotyczącą trzech kolejnych wyrazów ciągu geometrycznego:
![]()
Oczywiście liczbą o indeksie n, będzie środkowa z podanych liczb, czyli 9, zaś odpowiednio pierwsza będzie liczbą o indeksie n-1, zaś trzecia – o indeksie n+1. Podstaw te liczby pod wyżej wspomnianą własność:
![]()
Oblicz, ile wynosi lewa strona.
![]()
Teraz musisz wyliczyć, ile wynosi prawa strona:
![]()
Aby obliczyć to wyrażenie potrzebujesz sprowadzić wszystkie składniki do tej samej podstawy. Łatwiej będzie przekształcić podstawę ![]()
![]()
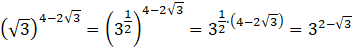
![]()
Teraz skorzystaj z własności mnożenia potęg o tych samych podstawach, czyli dodaj wykładniki:
![]()
Prawa strona wynosi tyle samo co lewa, co oznacza, że podstawione liczby spełniają wyjściową zależność. To z kolei oznacza, że te liczby są kolejnymi elementami ciągu geometrycznego, co należało wykazać.
Ponieważ kolejne wyrazy ciągu geometrycznego powstają przez pomnożenie poprzedniego przez iloraz, to aby obliczyć iloraz, wystarczy podzielić wyraz kolejnym przez poprzedni. Możesz podzielić wyraz drugi przez pierwszy lub trzeci przez drugi.
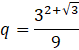
Aby określić, czy iloraz jest większy od 3, sprowadźmy to wyrażenie do postaci potęgi 3
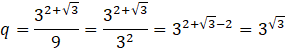
![]()
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
