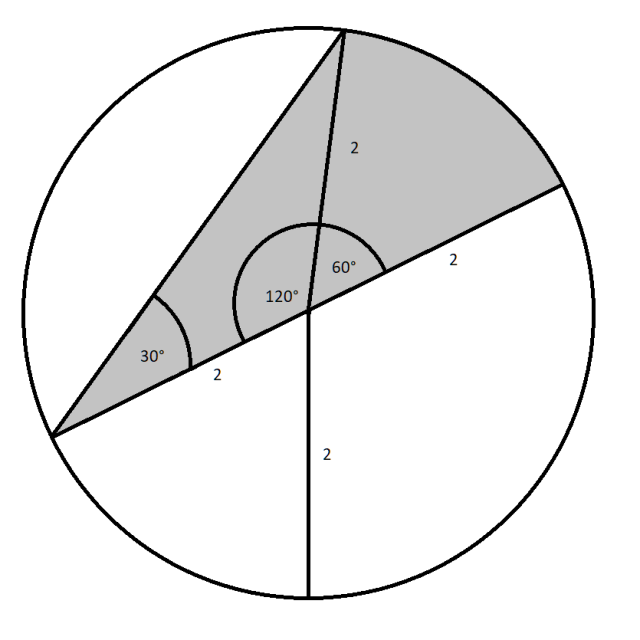
W tym zadaniu musisz obliczyć jaką wartość pola ma zacieniowana figura na poniższej ilustracji.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Odpowiedź: A. ![]()

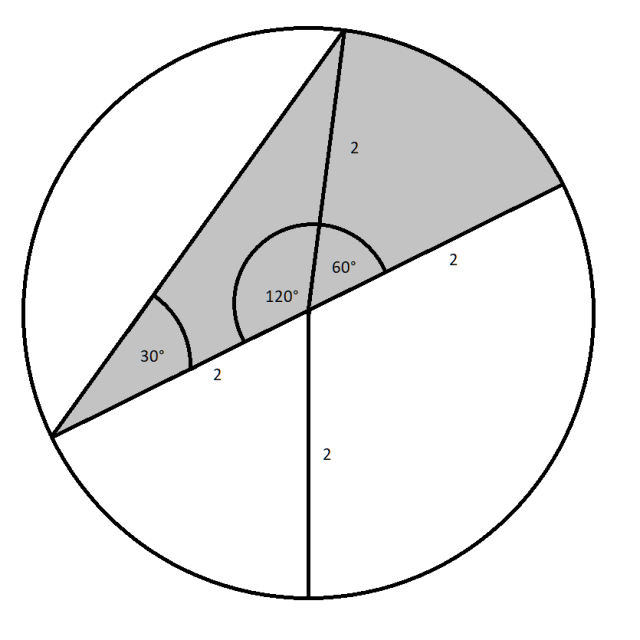
Dorysuj promień, który podzieli zacieniowaną figurę na trójkąt równoramienny oraz wycinek koła. Zauważ, że kąt znajdujący się w wycinku koła jest kątem środkowym opartym na tym samy łuku co kąt 30°. Więc jego miara jest dwukrotnie większa i wynosi 60°. Kąt między ramionami (które są promieniami okręgu) w trójkącie równoramiennym to kąt przyległy do kąta o mierze 60°. Ich miary mają dać łącznie 180°, więc kąt między ramionami w tym trójkącie musi mieć miarę 120°. Pole tego trójkąta możesz obliczyć ze wzoru, który wykorzystuje długości boków oraz sinus kąta między nimi. Podstawiając długości tych boków (czyli promień okręgu) oraz kąt 120° otrzymasz pole trójkąta.
![]()
Ponieważ wartość sin 120° nie znajduje się w żadnej tabelce, musisz obliczyć jego wartość. Użyj do tego wzorów redukcyjnych. Skorzystaj tutaj z tego, że:
![]()
Kąt 120° możesz zapisać jako 180° – 60°, więc kątem α ze wzoru będzie 60°.
![]()
Podstawiając do wzoru uzyskasz:
![]()
Pole wycinka koła obliczysz ze wzoru:
![]()
Gdzie β to kąt wewnątrz tego wycinka koła i w tym przypadku wynosi on 60°.
![]()
Oczywiście pole zacieniowanej figury to suma pól trójkąta równobocznego i wycinka koła.
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
