W tym zadaniu musisz wyznaczyć jaką objętość ma ostrosłup prawidłowy o siatce znajdującej się na załączonej ilustracji.
Ponieważ jest to ostrosłup prawidłowy, to jego podstawą jest trójkąt równoboczny, zaś ściany boczne to trójkąty równoramienne o ramieniu 10 i kącie między nimi 40°. Z twierdzenia cosinusów:
![]()
![]()
![]()
![]()
Wysokość ostrosłupa tworzy wraz z fragmentem wysokości podstawy oraz krawędzią boczną trójkąt prostokątny, w którym przeciwprostokątną jest krawędź boczna. Ponieważ jest to ostrosłup prawidłowy, to spodek wysokości jest środkiem okręgu opisanego na podstawie. W trójkącie równoramiennym promień okręgu opisanego to ![]()
Wysokość w trójkącie równoramiennym to ![]()
![]()
![]()
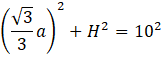
![]()
![]()
![]()
![]()

Do obliczenia objętości ostrosłupa potrzebujesz pola powierzchni jego podstawy oraz wysokości.
Ponieważ jest to ostrosłup prawidłowy, to jego podstawą jest trójkąt równoboczny. Więc aby obliczyć jego pole wystarczy znać długość jego boku. Zauważ, że ściany boczne są trójkątami równoramiennymi o ramieniu 10 i kącie między nimi 40°. Szukany bok jest naprzeciw tego kąta. Jeśli oznaczysz go jako a, możesz go więc obliczyć z twierdzenia cosinusów, które będzie miało postać w tym przypadku:
![]()
Wartość cosinusa musisz odczytać z tablic wartości funkcji trygonometrycznych.
![]()
![]()
Zauważ, że dalej będziesz potrzebował jedynie a2, a nie samego a, więc nie ma sensu wyliczać a.
Pole powierzchni podstawy obliczysz ze wzoru na pole trójkąta równobocznego. Zauważ, że w obliczeniach przed długością boku, pojawiła się ta długość w kwadracie. Wykorzystaj ją w obliczeniu pola powierzchni podstawy.
![]()
Zauważ, że wysokość ostrosłupa tworzy wraz z fragmentem wysokości podstawy oraz krawędzią boczną trójkąt prostokątny, w którym przeciwprostokątną jest krawędź boczna. Ponieważ jest to ostrosłup prawidłowy, to spodek wysokości jest środkiem okręgu opisanego na podstawie. W trójkącie równoramiennym promień okręgu opisanego to ![]()
Wysokość w trójkącie równoramiennym to ![]()
![]()
![]()
Korzystając z twierdzenia Pitagorasa możesz obliczyć wysokość ostrosłupa.
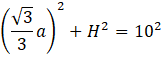
![]()
![]()
Oczywiście możesz odrzucić ujemną wysokość.
![]()
Mając te informacje możesz skorzystać ze wzoru na objętość ostrosłupa:
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
