W tym zadaniu musisz obliczyć dla jakich liczb wszystkie podane nierówności są spełnione.
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

$\text{[math]}$

Brak miejsc zerowych, a > 0, więc nierówność zawsze spełniona

$\text{[math]}$ .

Liczby, które spełniają wszystkie trzy nierówności na raz:

$\text{[math]}$

Aby określić które liczby spełniają wszystkie podane nierówności, musisz rozwiązać każdą z nich z osobna, a następnie wziąć część wspólną wszystkich rozwiązań. W każdej nierówności musisz wyznaczyć miejsca zerowe a następnie narysować odpowiedni rysunek, aby wyznaczyć odpowiedni przedział.

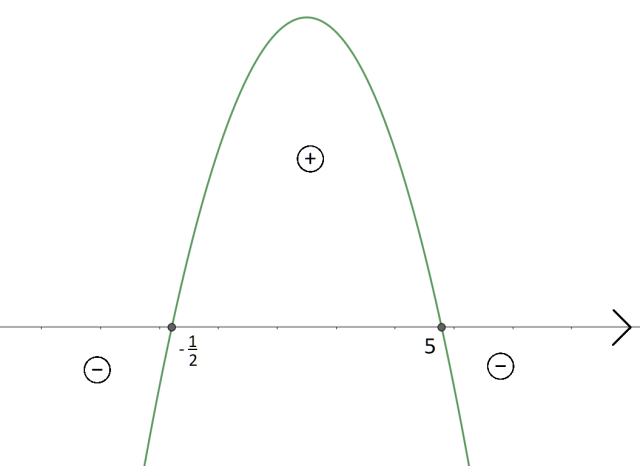
$\text{[math]}$ Masz tu do czynienia prawie z postacią iloczynową funkcji kwadratowej. Przyrównując obydwa nawiasy do 0 otrzymasz miejsca zerowe.

$\text{[math]}$

Aby określić jaki znak ma współczynnik a, przemnóż przez siebie współczynniki stojące przy x w każdym nawiasie. Będzie to 2 ∙ (-1) = -2, a więc liczba ujemna. Oznacza to, że parabola ma ramiona skierowane ku dołowi.

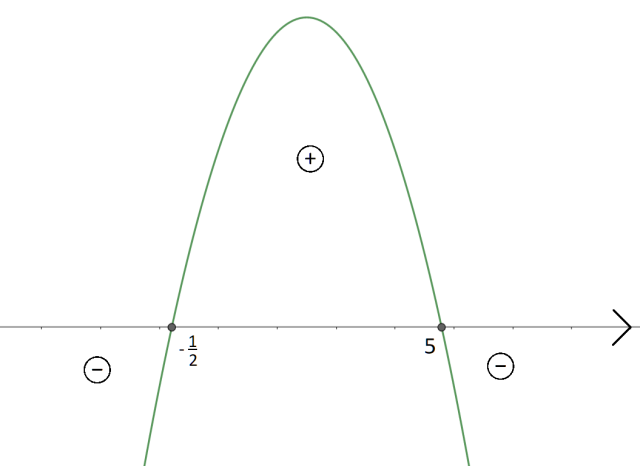
Ponieważ w nierówności ta funkcja ma być większa lub równa 0, to interesuje cię przedział, w którym wartości funkcji są dodatnie wraz z miejscami zerowymi. Z wykresu możesz odczytać, że będzie to przedział:

$\text{[math]}$

Aby rozwiązać tę nierówność musisz najpierw wymnożyć nawias a następnie przenieść wszystkie składniki na jedną stroną.

$\text{[math]}$

Zauważ, że środkowy składnik możesz zapisać jako 2 ∙ 4 ∙ x, zaś 16 jako x².

$\text{[math]}$

Masz tu do czynienia ze wzorem skróconego mnożenia na kwadrat różnicy, gdzie a = x, zaś b = 4. Zwijając to ze wzoru, otrzymasz:

$\text{[math]}$

Kwadrat dowolnej liczby jest zawsze liczbą większą od zera, więc tę nierówność spełniają wszystkie liczby rzeczywiste. Jednak prawa strona ma być większa od 0, zaś dla x = 4 prawa strona się zeruje, więc akurat dla tego x nierówność nie jest spełniona. Podsumowując rozwiązaniem tej nierówności jest:

$\text{[math]}$

Podobnie jak wcześniej musisz wymnożyć wszystkie nawiasy i przenieść wszystko na jedną stronę.

$\text{[math]}$

Delta wyszła ujemna, więc funkcja nie ma miejsc zerowych. Jednak to nie koniec rozwiązywania nierówności. Skoro współczynnik a jest dodatni to funkcja ma ramiona są skierowane ku górze, a skoro funkcja nie ma miejsc zerowych to nie przecina osi OX, więc ciągle jest dodatnia. W nierówności masz sprawdzić, czy funkcja jest większa od zera. Oznacza to, że tę nierówność spełniają także wszystkie liczby rzeczywiste, co możesz zapisać:

$\text{[math]}$ .

Aby wyznaczyć liczby, które spełniają wszystkie równania jednocześnie musisz wziąć część wspólną wszystkich trzech zbiorów.

$\text{[math]}$

Zauważ, że ostatnie dwa zbiory to prawie wszystkie liczby z wyjątkiem 4. Więc część wspólna tych wszystkich trzech zbiorów to ten pierwszy zbiór, ale bez 4, co możesz zapisać jako:

Matematyka z Plusem. Klasa 4. Podręcznik – rozwiązania i odpowiedzi

Zadanie 16. - strona 107

Zadanie

W tym zadaniu musisz obliczyć dla jakich liczb wszystkie podane nierówności są spełnione.

Rozwiązanie

Wyjaśnienie

Matematyka - wybrane pytania

W tym zadaniu musisz obliczyć dla jakich liczb wszystkie podane nierówności są spełnione.
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$