W tym zadaniu musisz wskazać fałszywe zdanie dotyczące układu równań ![]()
![]()
![]()
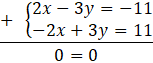
Układ jest nieoznaczony.
![]()
![]()
Dowolna para liczb, spełniająca powyższą równość, jest rozwiązaniem tego układu. Jednakże, to nie może być dowolna para liczb. Np. x=0 i y=0 nie jest rozwiązaniem tego układu równań, bo 0≠0 – 11
Odpowiedź: D. Dowolna para liczb, jest rozwiązaniem tego układu równań.

Zauważ, że każde ze zdań których prawdziwość masz sprawdzić, dotyczy rozwiązań tego układu równań. Dlatego musisz go rozwiązać. Aby łatwiej było na nim pracować, warto każde równanie doprowadzić do postaci takiej, że po jednej stronie równania są uporządkowane alfabetycznie niewiadome, a po drugiej liczby. Robisz to przez odpowiednie przenoszenie składników na drugą stronę.
![]()
![]()
Zauważ, że po przemnożeniu drugiego równania przez 2, współczynniki stojące przy x będą tymi samymi liczbami, tylko z przeciwnymi znakami. Będzie można zastosować metodę przeciwnych współczynników.
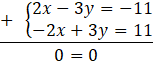
Po dodaniu stronami obydwu równań okazuje się, że otrzymujesz 0=0. Oznacza to, że układ ma nieskończenie wiele rozwiązań, czyli jest układem nieoznaczonym. Pamiętaj jednak, że nieskończona liczba rozwiązań, nie oznacza, że każda para liczb jest rozwiązaniem, a jedynie te liczby, które spełniają któreś z dwóch równań. Wyznacz z któregoś tych równań x w zależność od y (albo y w zależności od x)
![]()
![]()
Warto znaleźć przykład pary liczb, która nie jest rozwiązaniem tego układu równań, aby ostatecznie pokazać, że ostatnie zdanie jest fałszywe (Dowolna para liczb, jest rozwiązaniem tego układu równań). Najprostszym takim kontrprzykładem jest para liczb x=0 i y=0, gdyż 0 ≠ 0 – 11.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
