W tym zadaniu musisz udowodnić, że zachodzi własność:
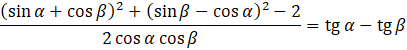
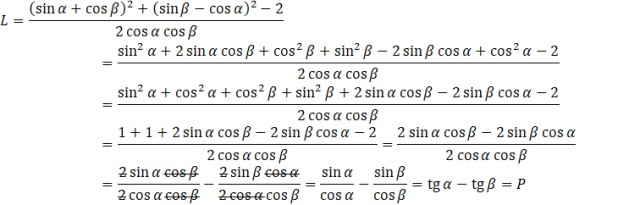
Co kończy dowód.

Aby dowieść prawdziwości tożsamości wystarczy, że pokażesz, że lewą stronę można przekształcić w prawą stronę, bądź na odwrót (ewentualnie, że obie strony da się przekształcić w takie same wyrażenia). W tym wypadku warto przekształcić lewą stronę.
Lewą stronę możesz rozpisać jako:
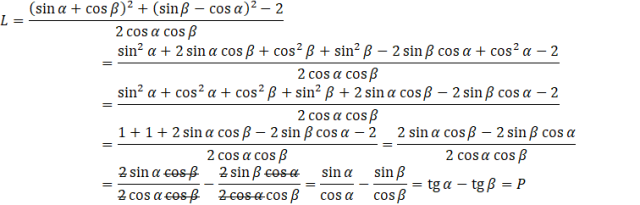
Na początku korzystając ze wzorów skróconego mnożenia, wymnażasz nawiasy które są podniesione do kwadratów. Następnie musisz uporządkować wyrażenia w liczniku. Zauważ, że otrzymujesz dwie jedynki trygonometryczne. Jednakże redukują się one z -2. Otrzymany ułamek, który ma w liczniku różnicę, możesz rozbić na różnicę dwóch ułamków. Po skróceniu się tych samych wyrazów otrzymasz dwa ułamki, gdzie każdy to iloraz sinusa i cosinusa tego samego kąta. Takie wyrażenie możesz zapisać jako tangens danego kąta. W ten sposób otrzymałeś prawą stronę tożsamości, co kończy dowód.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
