W tym zadaniu musisz obliczyć prawdopodobieństwo, że przy rzucie dwiema kostkami sześciennymi, po zsumowaniu liczby oczek na każdej z nich otrzymasz liczbę mniejszą od 10.
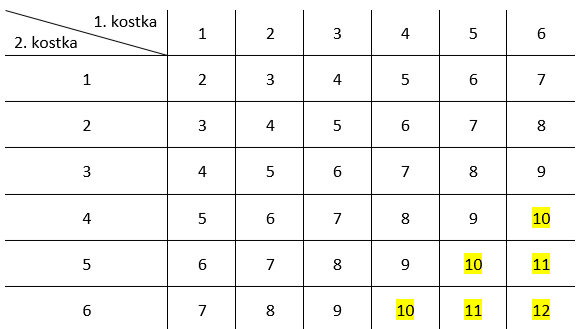
A – wyrzucono sumę oczek mniejszą od 10
A’ – wyrzucono sumę oczek większą lub równą 10
N = 6 ∙ 6 = 36
nA = 6
![]()
![]()
![]()
Odp.: D. ![]()

Na początku dobrze jest określić co jest tutaj zdarzeniem losowym. Jest to takie wyrzucenie kostek, że suma oczek na nich jest mniejsza od 10. Oznacz to zdarzenie jako A. Zauważ, że łatwiej będzie tutaj skorzystać ze zdarzenia przeciwnego, którym jest wyrzucenie takiej ilości oczek, że ich suma jest większa lub równa 10. Jest to zdarzenie A’. Najlepszym rozwiązaniem tutaj jest narysowanie tabeli z wszystkimi możliwymi sumami rzutów kostek oraz wypełnienie jej tymi sumami (aby łatwiej było zaznaczyć). Następnie zaznacz te sumy, które są większe lub równe od 10.
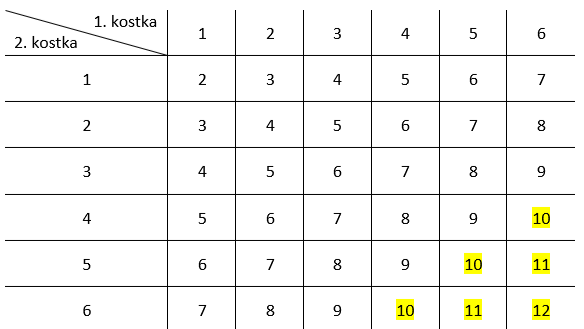
Zauważ, że cała tabela reprezentuje przestrzeń zdarzeń elementarnych, więc musisz policzyć, ile jest komórek w tabeli. Najszybciej to zrobisz przez pomnożenie ilości wierszy i komórek. Jest ich 6 ∙ 6, czyli 36. Natomiast zdarzeniem losowym będą zaznaczone przez ciebie rzuty. Jest ich 6. Teraz korzystasz z klasycznej definicji prawdopodobieństwa.
![]()
Pamiętaj, że jest to prawdopodobieństwo zdarzenia przeciwnego. Aby obliczyć prawdopodobieństwo zdarzenia A, musisz skorzystać z definicji prawdopodobieństwa zdarzenia przeciwnego.
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
