W tym zadaniu musisz określić jak wiele jest razy większy obwód kwadratu wpisanego w pewien okrąg, od obwodu trójkąta równobocznego wpisanego w ten sam okrąg.
![]()
Gdzie R to promień rozważanego okręgu.
![]()
Gdzie a to długość boku trójkąta.
![]()
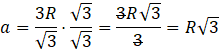
![]()
![]()
Gdzie d to przekątna kwadratu
![]()
Gdzie b to długość boku kwadratu.
![]()
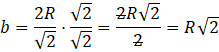
![]()
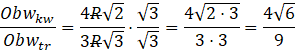
Odpowiedź: D. ![]()

Promień okręgu opisanego na trójkącie równobocznym (skoro wpisano trójkąt w okrąg, to ten okrąg jest okręgiem opisanym na trójkącie) wynosi ![]()
![]()
Gdzie R to promień rozważanego okręgu. W trójkącie równobocznym zachodzi:
![]()
Gdzie a to długość boku trójkąta. Podstawiając to do wzoru na promień okręgu opisanego otrzymasz zależność między R oraz a.
![]()
Jednakże to promień okręgu jest ustalony, więc warto wyznaczyć a w zależności od R. Zrobisz to przez pomnożeniu obu stron przez ![]()
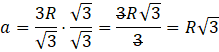
Obwód trójkąta to suma jego trzech boków. Ponieważ w trójkącie równobocznym wszystkie boki są sobie równe, to sprowadza się to do pomnożenia długości boku przez 3.
![]()
Promień okręgu opisanego na kwadracie, to z kolei połowa jego przekątnej co możesz zapisać jako:
![]()
Długość przekątnej z kolei wyraża się wzorem:
![]()
Gdzie b to długość boku kwadratu. Podstawiając to do wzoru na promień otrzymasz zależność między R oraz b.
![]()
Podobnie jak wcześniej, warto wyznaczyć, jak zależy b od R przez pomnożenie obu stron przez ![]()
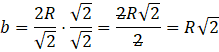
Ponieważ w mianowniku pojawia się pierwiastek, musisz usunąć niewymierność przez przemnożenie licznika i mianownika przez ten pierwiastek.
Obwód kwadratu to suma jego czterech boków. Ponieważ w kwadracie wszystkie boki są sobie równe, to sprowadza się to do pomnożenia długości boku przez 4.
![]()
Aby wyznaczyć, ile razy jest większy obwód kwadratu od obwodu trójkąta musisz określić, ile obwodów trójkąta mieści się w obwodzie kwadratu. Aby to obliczyć musisz podzielić obwód kwadratu przez obwód trójkąta.
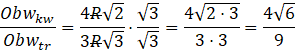

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
