W tym zadaniu musisz wyliczyć, ile wynosi wartość kąta ABC w trójkącie, który jest wyznaczony przez wierzchołki ![]()
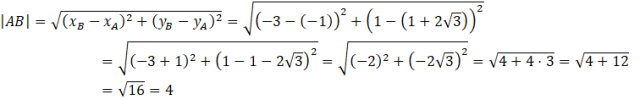
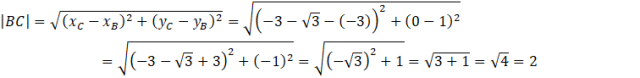
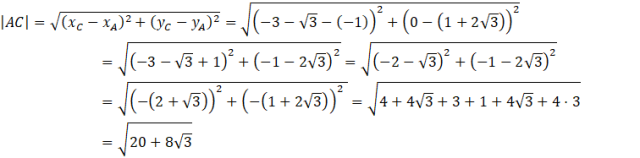
Z twierdzenia cosinusów:
![]()
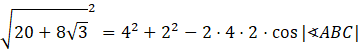
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Kąt ABC możesz wyznaczyć z twierdzenia cosinusów. Jednakże najpierw, aby skorzystać z tego twierdzenia musisz wyznaczyć długości boków tego trójkąta. W tym celu skorzystać ze wzoru na długość odcinka pomiędzy dwoma punktami.
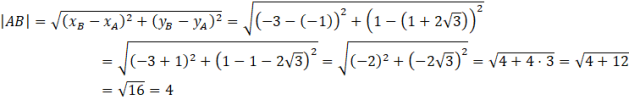
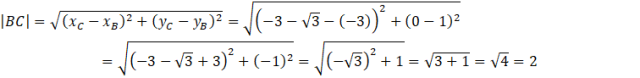
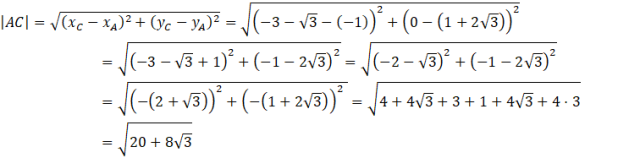
Przy liczeniu |AC| skorzystałeś ze wzoru skróconego mnożenia. Jednakże, aby móc go zastosować, musiałeś wyciągnąć minusy z obu nawiasów. Pamiętaj, że po wyciągnięciu minusa, on zostaje pod kwadratem. Po podniesieniu do kwadratu -1 daje 1, co oznacza, że minus znika.
Teraz podstaw otrzymane wzory do twierdzenia cosinusów. Kąt ABC jest naprzeciwko boku AC.
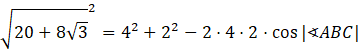
![]()
![]()
![]()
![]()
Ponieważ cosinus wyszedł ci ujemny, to aby wyznaczyć kąt ABC musisz skorzystać ze wzorów redukcyjnych. Skorzystaj tutaj z tego, że:
![]()
Więc otrzymany cosinus możesz zapisać jako cosinus pewnego kąta (niech to będzie α) ze znakiem minus.
![]()
![]()
![]()
Z tablic wartości trygonometrycznych możesz odczytać, że kąt α ma wartość 30°. Oznacza to, że kąt ABC ma wartość 180° – 30° = 150°

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
