W tym zadaniu musisz obliczyć dla których argumentów funkcja f(x) = x2 – 3x – 4 osiąga większe wartości niż funkcja g(x) = 2x + 10.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
I to właśnie dla tych argumentów funkcja f ma większe wartości niż g.

Rozwiązanie zadania sprowadza się do rozwiązania nierówności:
![]()
Podstawiając wzory funkcji otrzymasz nierówność:
![]()
Którą rozwiązujesz jak standardową nierówność kwadratową. Najpierw musisz wyznaczyć miejsca zerowe, a potem naszkicować przybliżony wykres.
![]()
![]()
![]()
![]()
![]()
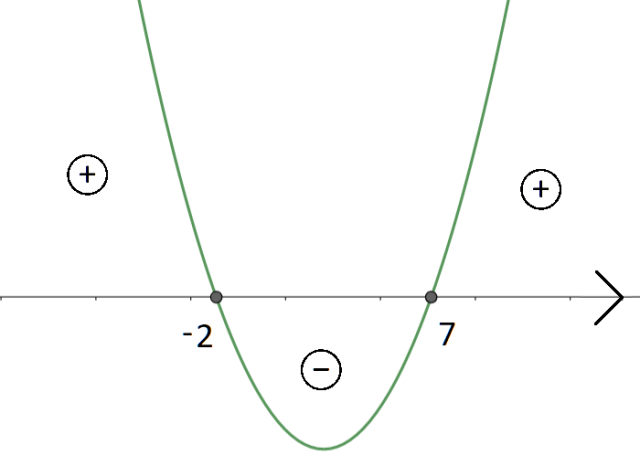
Teraz naszkicuj wykres. Ponieważ współczynnik a jest większy od 0, to ramiona tej paraboli będą skierowane ku górze.
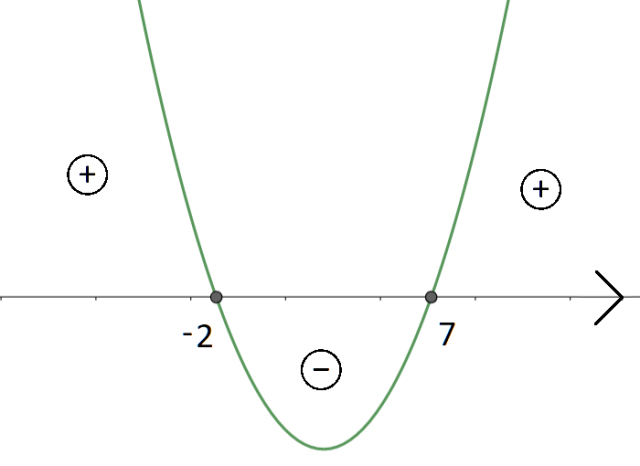
Ponieważ, w nierówności funkcja ma być większa od zera, to rozwiązaniem tej nierówności są te przedziały, dla których funkcja jest większa od zera. Pamiętaj, że w tym przypadku nie uwzględniasz miejsc zerowych.
![]()
I to właśnie dla tych argumentów funkcja f ma większe wartości niż g.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
