W tym zadaniu musisz obliczyć stosunek promienia podstawy stożka, którego powierzchnię boczną stanowi wycinek koła o mierze kąta środkowego wynoszącej 90° do promienia podstawy stożka, którego powierzchnię boczną stanowi pozostała część wspomnianego wcześniej koła.
![]()
![]()
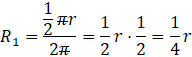
360° – 90° = 270°.
![]()
![]()
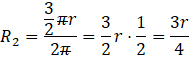
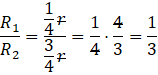
Odpowiedź: B. ![]()

Niech promień koła, z którego wycinano powierzchnie boczne obu stożków wynosi r. Wtedy długość łuku pierwszego wycinku wynosi:
![]()
Ta długość łuku jest także obwodem koła będącego podstawą stożka otrzymanego z tego wycinku. Możesz więc przyrównać tę długość łuku do wzoru na obwód koła:
![]()
Z tego równania wyznacz R1 przez podzielenie obu stron przez 2π.
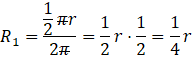
Analogicznie postąp dla drugiego stożka. Kąt środkowy pozostałego wycinka koła wynosi: 360° – 90° = 270°.
![]()
Podobnie jak wcześniej przyrównaj otrzymaną długość łuku do obwodu podstawy drugiego walca.
![]()
Wyznacz R2 z tego równania.
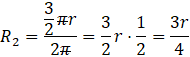
Teraz musisz policzyć stosunek tych dwóch promieni.
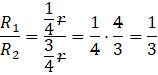

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
