W tym zadaniu musisz określić, ile musi wynosić wartość parametru p, aby wielomian W(x) = x3 + px2 – 3x – 18 dzielił się bez reszty przez wielomian x + 3. Gdy już wyznaczysz szukany parametr wyznacz jeszcze x spełniające równanie W(x) = 0.
Jeśli wielomian W(x) ma się dzielić bez reszty przez x + 3, to na podstawie twierdzenia o reszcie wielomianu z dzielenia przez dwumian postaci x – a musi zachodzić równość:
![]()
![]()
![]()
![]()
![]()
Więc wielomian W(x) jest podzielny przez x + 3, dla p = 4. Wielomian W(x) ma wtedy postać:
![]()
Oczywiście jednym z rozwiązań równania W(x) = 0 jest -3, co wynika z treści zadania i twierdzenia o reszcie wielomianu. Zauważ, że rozwiązaniami tego równania są po prostu pierwiastki wielomianu W(x), więc zadanie sprowadza się do ich znalezienia. Jeśli podzielisz W(x) przez x + 3 otrzymasz wielomian kwadratowy, którego pierwiastki łatwo jest znaleźć.
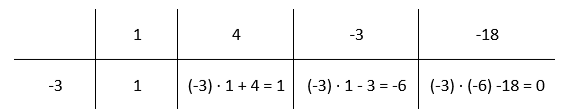
![]()
![]()
![]()
![]()
![]()
Więc rozwiązaniami równania W(x) = 0 są: -3 oraz 2

Jeśli wielomian W(x) ma się dzielić bez reszty przez x + 3, to na podstawie twierdzenia o reszcie wielomianu z dzielenia przez dwumian postaci x – a (a możesz tu stosować to twierdzenie, gdyż x + 3 jest takim dwumianem, gdzie a = -3) musi zachodzić równość:
![]()
Gdyż oczywiście reszta ma wynosić 0. Oznacz to, że po podstawieniu x = 3, powinieneś otrzymać 0. Ponieważ w wielomianie występuje parametr p, to jeśli podstawisz x = 3 oraz przyrównasz to do 0, to otrzymasz proste równanie z p, po którego rozwiązaniu otrzymasz szukaną wielkość.
![]()
![]()
![]()
![]()
Więc wielomian W(x) jest podzielny przez x + 3, dla p = 4. Wielomian W(x) ma wtedy postać:
![]()
Oczywiście jednym z rozwiązań równania W(x) = 0 jest -3, co wynika z treści zadania i twierdzenia o reszcie wielomianu. Zauważ, że rozwiązaniami tego równania są po prostu pierwiastki wielomianu W(x), więc zadanie sprowadza się do ich znalezienia. Jeśli podzielisz W(x) przez x + 3 otrzymasz wielomian kwadratowy, którego pierwiastki łatwo jest znaleźć. Aby podzielić wielomian W(x) przez x + 3 skorzystaj ze schematu Hornera.
Narysuj tabelę i w pierwszym wierszu wpisz współczynniki przy kolejnych potęgach wielomianu W(x), zaś w pierwszej komórce wiersza drugiego wpisz współczynnik a. W tym przypadku wynosi on -3. Kolejne komórki w drugim wierszu będziesz uzyskiwał, przez przemnożenie poprzedniej komórki w drugim wierszu przez a, a następnie dodanie zawartości komórki w wierszu powyżej. Drugą komórkę w drugim wierszu uzupełniasz przez przepisanie wartości wyżej.
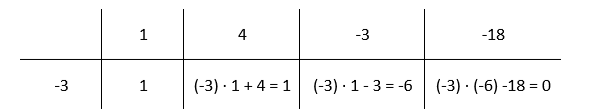
Więc wielomian, który otrzymasz w wyniku W(x): (x + 1) to x2 + x – 6.
Aby znaleźć pierwiastki tego wielomianu kwadratowego wystarczy, że obliczysz Δ i skorzystasz ze wzorów na pierwiastki równania kwadratowego.
![]()
![]()
![]()
![]()
Więc rozwiązaniami równania W(x) = 0 są: -3 oraz 2

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
