W tym zadaniu musisz obliczyć prawdopodobieństwo, że przy losowaniu dwóch banknotów z dwóch przegródek portfela, gdzie w jednej z nich są dwa banknoty 10 zł, dwa 20 zł oraz jeden 50 zł, zaś w drugim jest jeden banknot 50 zł, dwa 100 zł i jeden 200 zł, wylosujesz kwotę większą niż 120 zł.
A wylosowanie dwóch banknotów, których suma jest większa niż 120 zł.
N = 5 ∙ 4 = 20
nA = 7
![]()
Odp.: B. ![]()

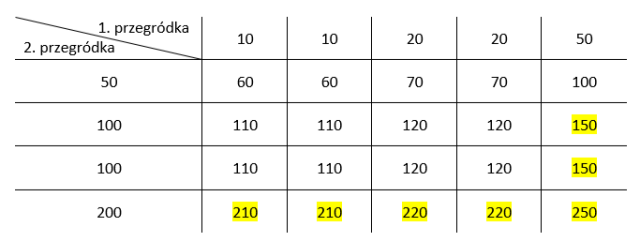
Na początku dobrze jest określić co jest tutaj zdarzeniem losowym. Jest to takie wylosowanie dwóch banknotów, że ich suma jest większa niż 120 zł. Oznacz to zdarzenie jako A. Najlepszym rozwiązaniem tutaj jest narysowanie tabeli z wszystkimi możliwymi wynikami losowań dwóch banknotów. Wypełnij tę tabelę sumami nominałów tych banknotów. Następnie zaznacz te pary nominałów, w których ich suma jest większa od 120 zł. Pamiętaj, że nawet jeśli nominały banknotów są te same, ale banknotów jest więcej to dla każdego banknotu musisz zarezerwować jedną kolumnę lub wiersz.
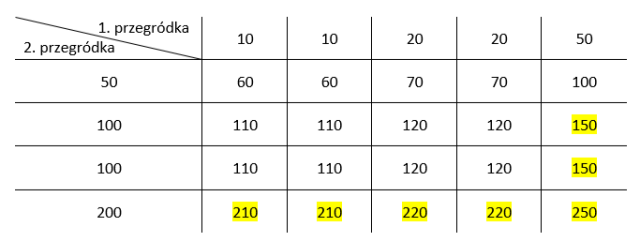
Zauważ, że cała tabela reprezentuje przestrzeń zdarzeń elementarnych, więc musisz policzyć, ile jest komórek w tabeli. Najszybciej to zrobisz przez pomnożenie ilości wierszy i komórek. Jest ich 5 ∙ 4, czyli 20. Natomiast zdarzeniem losowym będą zaznaczone przez ciebie kombinacje banknotów. Jest ich 7. Teraz korzystasz z klasycznej definicji prawdopodobieństwa.
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
