W tym zadaniu musisz obliczyć sumę pierwszej ósemki wyrazów ciągu geometrycznego (an) którego wzór ogólny wynosi ![]()
![]()
![]()
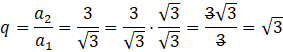
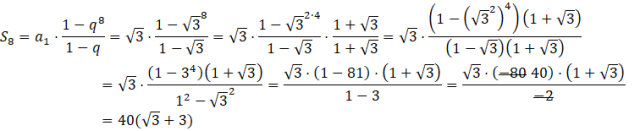
Odpowiedź: A. ![]()

Aby skorzystać ze wzoru na sumę pierwszych n wyrazów ciągu geometrycznego potrzebujesz a1 i q. Pierwszy wyraz wyznaczysz na podstawie wzoru ogólnego podstawiając n = 1:
![]()
Ponieważ, każdy kolejny wyraz ciągu geometrycznego powstaje przez pomnożenie wyrazu poprzedniego przez iloraz tego ciągu, to dzieląc wyraz następny przez poprzedni otrzymasz iloraz. Wystarczy więc policzyć następny wyraz a1, czyli a2, a następnie podzielić a2 przez a1. Wyraz a2 obliczasz podobnie jak a1, ze wzoru podanego w treści zadania.
![]()
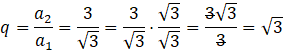
Pamiętaj, że gdy otrzymasz pierwiastek w mianowniku należy go z niego usunąć, przez pomnożenie licznika i mianownika przez usuwany pierwiastek.
Mając a1 oraz q, możesz obliczyć S8:
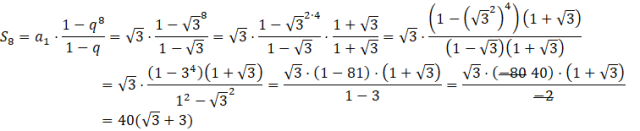
Aby obliczyć tę sumę pamiętaj o podstawowych własnościach potęg i pierwiastków. Pamiętaj, że gdy w mianowniku jest wyrażenie z pierwiastkiem, musisz pomnożyć licznik i mianownik przez to samo wyrażenie tylko, że ze zmienionym znakiem między liczbą a pierwiastkiem. Robi się to w celu, aby w mianowniku uzyskać wzór skróconego mnożenia, który wyeliminuje pierwiastek z mianownika.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
