W tym zadaniu musisz obliczyć pozostałe pierwiastki równania 2x3 + 2x2 – 5x – 2 = 0, wiedząc, że -2 jest jednym z nich.
Jeśli -2 jest pierwiastkiem wielomianu po lewej stronie równania, to na mocy twierdzenia odwrotnego do twierdzenia Bézouta, wielomian ten jest podzielny przez dwumian x – (-2), czyli x + 2.
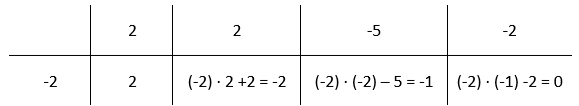
![]()
Więc równanie z treści zadania można zapisać jako:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Odpowiedź: D. ![]()

Jeśli -2 jest pierwiastkiem wielomianu po lewej stronie równania, to na mocy twierdzenia odwrotnego do twierdzenia Bézouta, wielomian ten jest podzielny przez dwumian x – (-2), czyli x + 2. W wyniku tego dzielenia otrzymasz wielomian stopnia drugiego, którego pierwiastki możesz obliczyć przy użyciu Δ.
Aby podzielić wielomian wyjściowy przez dwumian x + 2 warto skorzystać ze schematu Hornera. Schemat Hornera wykorzystuje się właśnie przy dzieleniu wielomianu przez dwumian w postaci x – a. Narysuj tabelę i w pierwszym wierszu wpisz współczynniki przy kolejnych potęgach wielomianu wyjściowego, zaś w pierwszej komórce wiersza drugiego wpisz współczynnik a. W tym przypadku wynosi on -2. Kolejne komórki w drugim wierszu będziesz uzyskiwał, przez przemnożenie poprzedniej komórki w drugim wierszu przez a, a następnie dodanie zawartości komórki w wierszu powyżej. Drugą komórkę w drugim wierszu uzupełniasz przez przepisanie wartości wyżej.
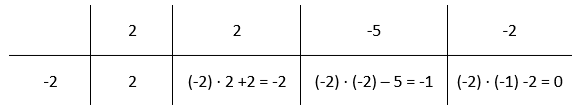
Wynikiem tego dzielenia będzie wielomian o jeden stopień niższy, a więc drugiego stopnia. Poszczególne komórki drugiego wiersza odpowiadają współczynnikom przy kolejnych potęgach wyniku, z kolei ostatnia komórka, to reszta z dzielenia. Ponieważ wielomian wyjściowy miał być podzielny przez x + 2, to reszta wynosząca 0 jest potwierdzeniem poprawności obliczeń. Z tego wynika, że wynik tego dzielenia to:
![]()
Więc równanie z treści zadania możesz zapisać jako:
![]()
Ponieważ jest to iloczyn wynoszący 0, to któryś ze składników wynosi 0.
![]()
Z pierwszego równania otrzymujesz znany pierwiastek, zaś drugie musisz rozwiązać jak standardowe równanie kwadratowe:
![]()
![]()
![]()
![]()
![]()
W odpowiedziach jest to pierwsze rozwiązanie (odpowiedź A. jest zbliżona do drugiego, ale w mianowniku jest 4).

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
