W tym zadaniu musisz określić jak wiele jest elementów ciągu (an) wyrażonego wzorem an = n(n – 14), takich, że są one mniejsze od 15.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Odpowiedź: B. 14.

Aby rozwiązać to zadanie stwórz nierówność, w której po jednej stronie będzie n-ty element, zaś po drugiej 15.
![]()
![]()
Wymnóż nawias oraz przenieś 15 na drugą stronę:
![]()
Otrzymujesz nierówność kwadratową. Aby ją rozwiązać oblicz miejsca zerowe funkcji po lewej stronie.
![]()
![]()
![]()
![]()
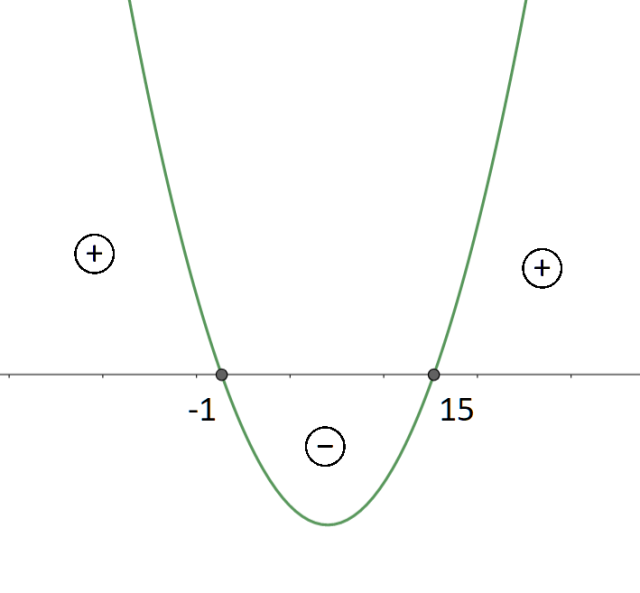
Mając miejsca zerowe narysuj pomocniczy rysunek, aby określić przedział, który będzie spełniał tę nierówność. Zwróć uwagę na współczynnik a, który jest dodatni, więc narysowana parabola musi mieć ramiona w górę.
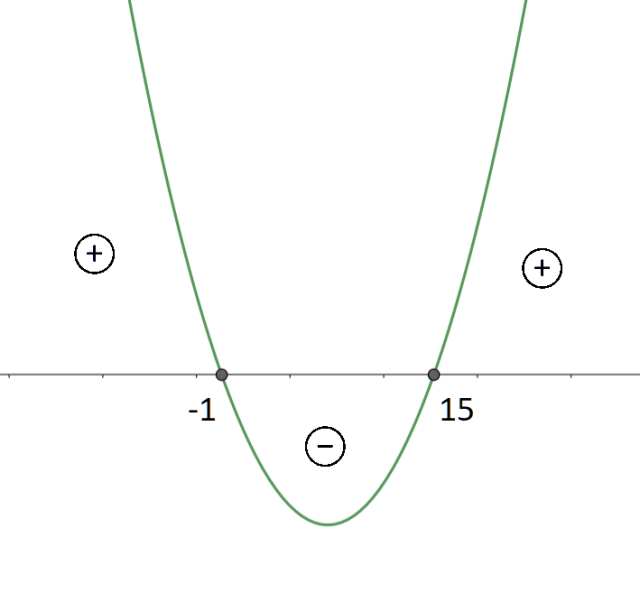
Ponieważ w nierówności ta funkcja ma być mniejsza od 0, to interesuje cię przedział, w którym wartości funkcji są ujemne. Z wykresu możesz odczytać, że będzie to przedział:
![]()
Przedziały otwarte, gdyż w nierówności wartości zerowe nie mają być uwzględniane. Pamiętaj, że pracujesz na ciągu, więc interesują cię tylko naturalne rozwiązania, więc wypisz liczby naturalne z otrzymanego przedziału:
![]()
Tych liczb jest 14.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
