Wykaż, że aby ramka zrobiona z drutu o długości d w kształcie równoległoboku o kącie ostrym α, ograniczała jak największe pole, powinna mieć kształt rombu.

a – długość jednego boku

b – długość drugiego boku

d = 2a + 2b – obwód równoległoboku, czyli długość drutu

$\text{[math]}$

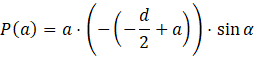
Funkcja kwadratowa, o miejscach zerowych x = 0 i x = $\text{[math]}$ . Współczynnik a ujemny (gdyż α jest kątem ostrym więc sin α > 0), więc osiąga wartość największą w wierzchołku paraboli będącej wykresem tej funkcji.

$\text{[math]}$

$\text{[math]}$ , więc równoległobok jest rombem, co należało udowodnić.

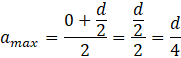
W pierwszej kolejności wypisz co wiesz na temat tej ramki. Oznacz jako a długość jej jednego boku, zaś jako b – długość drugiego boku. Wtedy długość całej ramki wyraża się wzorem:

$\text{[math]}$

Możesz z tego wzoru wyznaczyć zależność między np. b i a, przez przeniesienie a na drugą stronę:

2 $\text{[math]}$

$\text{[math]}$

Aby wyrazić pole równoległoboku ograniczonego przez tę ramkę skorzystaj ze wzoru na pole równoległoboku w zależności od długości boków i kąta między nimi:

$\text{[math]}$

Ale ponieważ, wyprowadziłeś wzór na b w zależności od a, to podstawiając za b otrzymasz zależność pola od odległości od ścianki (pamiętaj, że kąt jest ustalony, i tego sinusa możesz traktować jako pewną liczbę).

$\text{[math]}$

Zauważ, że jest to prawie postać iloczynowa funkcji kwadratowej. Aby w pełni była to ta postać, w żadnym nawiasie przy a nie mogą stać żadne liczby ani minusy (współczynnik przy a musi być równy 1). Aby to uzyskać musisz z pierwszego nawiasu wyciągnąć przed niego to, co stoi przy a, a więc -1. Robisz to dzieląc każdy składnik w nawiasie przez -1.

$\text{[math]}$

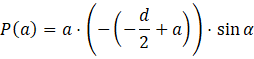
Dostałeś postać iloczynową funkcji kwadratowej, z której możesz odczytać miejsca zerowe tej funkcji. Jednym z nich jest $\text{[math]}$ (pamiętaj by przy odczycie miejsc zerowych z postaci iloczynowej zmienić znak na przeciwny). Z kolei, jeśli drugie b nie jest w żadnym nawiasie, to można je zapisać jako (b – 0), więc drugim miejscem zerowym jest 0 (ewentualnie można na to spojrzeć tak, że ta funkcja się zeruje dla b = 0)

Wyraziłeś pole rozważanego równoległoboku jako funkcję kwadratową boku a. Ponieważ współczynnik a (nie myl z bokiem a, tu chodzi o współczynnik we wzorach na funkcję kwadratową) jest ujemny (kąt α jest ostry, więc sinus tego kąta jest dodatni, co po przemnożeniu przez minus daje liczbę ujemną niezależnie od kąta), to parabola będąca wykresem tej funkcji ma ramiona skierowane w dół, a więc funkcja ta osiąga maksimum w wierzchołku tej paraboli. Więc aby obliczyć dla jakiej długości boku a pole rozważanego równoległoboku jest największe, wystarczy, że znajdziesz pierwszą współrzędną wierzchołka, oznaczaną jako p. Ponieważ znasz miejsca zerowe tej funkcji, to możesz wykorzystać wzór, który używa właśnie miejsc zerowych:

$\text{[math]}$

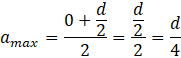
Musisz jeszcze obliczyć długość boku b. Robisz to przez podstawienie do wcześniej uzyskanego wzoru otrzymanego wyniku.

$\text{[math]}$

A więc długości boków równoległoboku, który ma największe pole są tej samej długości, więc ten równoległobok musi być rombem, co należało udowodnić.

Matematyka z Plusem. Klasa 4. Podręcznik – rozwiązania i odpowiedzi

Zadanie 27. - strona 108

Zadanie

Wykaż, że aby ramka zrobiona z drutu o długości d w kształcie równoległoboku o kącie ostrym α, ograniczała jak największe pole, powinna mieć kształt rombu.

Rozwiązanie

Wyjaśnienie

Matematyka - wybrane pytania