W tym zadaniu musisz wyznaczyć parametr p, tak aby wielomiany W(x) = 5x4 + 41x + 2 oraz Q(x) = -4x3 + px2 – 8 miały wspólny pierwiastek całkowity.
Wyznaczanie wspólnego pierwiastka całkowitego:
W(x) = 5x4 + 41x + 2
Spełnione są założenia twierdzenia o rozwiązaniach całkowitych. Wyraz wolny to 2. Dzielniki wyrazu wolnego to: 1, -1, 2 oraz -2.
![]()
Więc -2 jest pierwiastkiem wielomianu W(x).
Skoro -2 jest pierwiastkiem tego wielomianu, to oznacza, że wielomian ten jest podzielny przez dwumian x + 2.
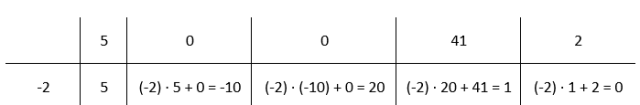
W(x): (x + 2) = 5x3 – 10x2 + 20x + 1.
Założenia twierdzenia o rozwiązaniach całkowitych są spełnione dla wyniku działania. Wyraz wolny to 1. Dzielnikami wyrazu wolnego są 1 oraz -1.
5 ∙ 13 – 10 ∙ 12 + 20 ∙ 1 + 1 = 5 – 10 + 20 + 1 = 16 ≠ 0
5 ∙ (-1)3 – 10 ∙ (-1)2 + 20 ∙ (-1) + 1 = -5 – 10 – 20 + 1 = -34 ≠ 0
Więc żaden z dzielników wyrazu wolnego nie jest pierwiastkiem tego wielomianu. Więc wielomian W(x) nie ma żadnych innych pierwiastków całkowitych. Co oznacza, że wspólnym pierwiastkiem całkowitym wielomianów W(x) i Q(x) będzie -2.
Aby -2 było pierwiastkiem wielomianu Q(x) musi zachodzić równość:
Q(-2) = 0
![]()
![]()
![]()
![]()
![]()

Aby rozwiązać to zadanie najpierw musisz określić jaki miałby być wspólny pierwiastek całkowity. Zauważ, że w pierwszym równaniu nie występuje parametr p, więc znajdując jego pierwiastki całkowite możesz określić który pierwiastek będzie tym wspólnym (na pewno któryś z pierwiastków pierwszego równania)
Zauważ, że pierwszego równania nie da się rozwiązać żadną „szybką” metodą. Jednak, ponieważ jest to wielomian o współczynnikach całkowitych możesz skorzystać z twierdzenia o rozwiązaniach całkowitych. Mówi ono o tym, że dla wielomianu o wszystkich współczynnikach są całkowitych (co jest spełnione) oraz takiego, że współczynniki przy najwyższej potędze i wyraz wolny są niezerowe (co także jest spełnione), to jeśli istnieją całkowite rozwiązania tego równania, to są one dzielnikami wyrazu wolnego.
Dla tego równania wyraz wolny to 2. Więc jego dzielnikami są liczby 1, -1, 2 oraz -2. Któraś z tych cyfr może być pierwiastkiem wielomianu. Musisz sprawdzić to podstawiając je (oczywiście jeśli masz podejrzenia, że któraś z tych liczb jest pierwiastkiem możesz zacząć od niej). Zauważ, że wszystkie składniki tego wielomianu są dodatnie, więc aby się wielomian wyzerował, musisz podstawić ujemnego x.
![]()
Więc -2 jest pierwiastkiem wielomianu W(x). Musisz jednak sprawdzić, czy nie ma innych liczb całkowitych będących pierwiastkami tego wielomianu.
Skoro -2 jest pierwiastkiem tego wielomianu, to oznacza, że wielomian ten jest podzielny przez dwumian x + 2 (pamiętaj, że we wzorze ogólnym jest x – a, zaś w tym przypadku a = -2, więc dostajesz x – (-2) = x + 2). Aby podzielić wielomian W(x) przez x + 2 skorzystaj ze schematu Hornera.
Narysuj tabelę i w pierwszym wierszu wpisz współczynniki przy kolejnych potęgach wielomianu W(x), zaś w pierwszej komórce wiersza drugiego wpisz współczynnik a. W tym przypadku wynosi on -2. Kolejne komórki w drugim wierszu będziesz uzyskiwał, przez przemnożenie poprzedniej komórki w drugim wierszu przez a, a następnie dodanie zawartości komórki w wierszu powyżej. Drugą komórkę w drugim wierszu uzupełniasz przez przepisanie wartości wyżej. Pamiętaj, że nawet jeśli wielomian nie zawiera x w pewnych potęgach, to musisz je uwzględnić, gdyż wtedy współczynniki przy tych potęgach wynoszą 0.
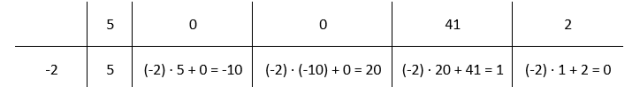
Więc wielomian, który otrzymasz w wyniku W(x): (x + 2) to 5x3 – 10x2 + 20x + 1.
Teraz wykorzystując to samo twierdzenie o rozwiązaniach całkowitych do wielomianu, który otrzymałeś możesz określić, czy istnieją jakieś inne pierwiastki wielomianu W(x). Wyraz wolny tego wielomianu to 1, więc jedynymi jego dzielnikami są 1 oraz -1. Aby sprawdzić czy to są pierwiastki tego wielomianu, wystarczy, że podstawisz je za x. Jeśli są to wyniki powinien ci wyjść 0.
5 ∙ 13 – 10 ∙ 12 + 20 ∙ 1 + 1 = 5 – 10 + 20 + 1 = 16 ≠ 0
5 ∙ (-1)3 – 10 ∙ (-1)2 + 20 ∙ (-1) + 1 = -5 – 10 – 20 + 1 = -34 ≠ 0
Więc żaden z dzielników wyrazu wolnego nie jest pierwiastkiem tego wielomianu. Więc ten wielomian nie ma żadnych innych pierwiastków całkowitych. Co oznacza, że wspólnym pierwiastkiem całkowitym wielomianów W(x) i Q(x) będzie -2.
Aby -2 było pierwiastkiem wielomianu Q(x) musi zachodzić równość:
Q(-2) = 0
Podstawiając x = -2 do wzoru na wielomian Q(x) otrzymasz:
![]()
![]()
![]()
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
