W tym zadaniu trzeba określić długość boku kwadratu, który należy wyciąć z rogów kartonu o kształcie kwadratu o boku a, aby prostopadłościenne pudełko, które powstanie po sklejeniu, miało jak największą powierzchnię boczną.

a – bok całego arkuszu

b – bok wyciętego rogu z arkusza

b x a – 2b – wymiary jednej ścianki bocznej pudełka powstałego w sposób opisany w treści zadania z arkusza

$\text{[math]}$ – pole ścianek bocznych pudełka

$\text{[math]}$

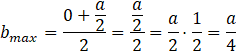
Jest to funkcja kwadratowa zmiennej b, o miejscach zerowych b = 0 i $\text{[math]}$ . Współczynnik a równania kwadratowego jest ujemny, więc funkcja osiąga wartość największą w wierzchołku paraboli będącej wykresem tej funkcji.

$\text{[math]}$

Więc powierzchnia ścianek bocznych pudełka powstałego w sposób opisany w zadaniu jest największa dla wyciętych kwadratów o boku $\text{[math]}$ długości boku arkusza.

Na początku oznacz przez b długość wycinanego kwadratu. Zastanów się jakie będzie pole powierzchni bocznej które będziesz chciał zmaksymalizować. Pole to składa się z czterech ścianek bocznych. Jeden bok każdej z takiej ścianki ma długość b, zaś drugi to długość boku a, pomniejszona o długość wyciętych kwadratów z każdej strony, czyli a – 2b. Pole powierzchni bocznej pudełka to cztery pola każdej ścianki, więc to pole wyraża się wzorem:

$\text{[math]}$

Zauważ, że jest to prawie postać iloczynowa funkcji kwadratowej, jeśli przyjmiesz b jako zmienną. Pamiętaj, że w tym zadaniu długość boku a jest ustalona, więc a musisz traktować jak zwykłą liczbę. Aby w pełni była to postać iloczynowa, w żadnym nawiasie przy b nie mogą stać żadne liczby ani minusy (współczynnik przy b musi być równy 1). Aby to uzyskać musisz z nawiasu wyciągnąć przed niego to, co stoi przy b, a więc -2. Robisz to dzieląc każdy składnik w nawiasie przez -2.

$\text{[math]}$

Oczywiście w pierwszym nawiasie możesz zmienić kolejność, skąd wprost możesz odczytać jedno miejsce zerowe tej funkcji kwadratowej, czyli $\text{[math]}$ (pamiętaj by przy odczycie miejsc zerowych z postaci iloczynowej zmienić znak na przeciwny). Z kolei, jeśli drugie b nie jest w żadnym nawiasie, to można je zapisać jako (b – 0), więc drugim miejscem zerowym jest 0 (ewentualnie można na to spojrzeć tak, że ta funkcja się zeruje dla b = 0)

Wyraziłeś pole powierzchni bocznej pudełka jako funkcję kwadratową boku b. Ponieważ współczynnik a (nie myl tego ze zmienną a, teraz chodzi o współczynnik przy kwadracie zmiennej w funkcji kwadratowej) jest ujemny, to parabola będąca wykresem tej funkcji ma ramiona skierowane w dół, a więc funkcja ta osiąga maksimum w wierzchołku tej paraboli. Więc aby obliczyć dla jakiej długości boku b rozważane pole powierzchni bocznej jest największe, wystarczy, że znajdziesz pierwszą współrzędną wierzchołka, oznaczaną jako p. Ponieważ znasz miejsca zerowe tej funkcji, to możesz wykorzystać wzór, który używa właśnie miejsc zerowych:

$\text{[math]}$

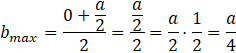
Więc powierzchnia ścianek bocznych pudełka powstałego w sposób opisany w zadaniu jest największa dla wyciętych kwadratów o boku $\text{[math]}$ długości boku arkusza.

Matematyka z Plusem. Klasa 4. Podręcznik – rozwiązania i odpowiedzi

Zadanie 24. - strona 137

Zadanie

W tym zadaniu trzeba określić długość boku kwadratu, który należy wyciąć z rogów kartonu o kształcie kwadratu o boku a, aby prostopadłościenne pudełko, które powstanie po sklejeniu, miało jak największą powierzchnię boczną.

Rozwiązanie

Wyjaśnienie

Matematyka - wybrane pytania