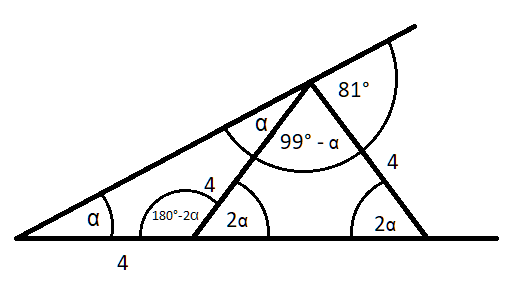
W tym zadaniu musisz obliczyć, ile wynosi kąt α z poniższej ilustracji.
![]()
![]()
![]()
Odpowiedź: B. 27°α.

Warto w tym zadaniu przerysować rysunek oraz zaznaczyć dodatkowe kąty.
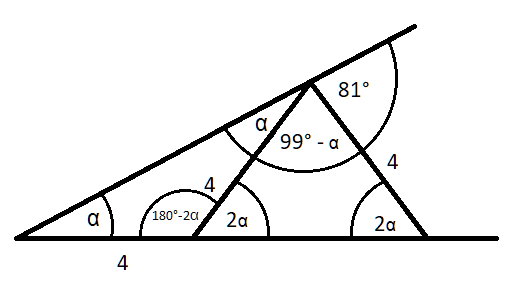
Trójkąt z lewej strony jest trójkątem równoramiennym, zaś kąt α jest kątem między ramieniem a podstawą tego trójkąta. W trójkącie równoramiennym oba kąty między ramieniem a podstawą mają tę samą miarę, wobec czego górny kąt w tym trójkącie także ma miarę α. Ponieważ suma kątów w trójkącie wynosi 180°, to trzeci kąt (czyli kąt między ramionami – dolny prawy) musi mieć miarę 180° – 2α.
Trójkąt z prawej strony również jest równoramienny, a więc kąty między jego podstawą a ramionami (dwa kąty dolne) są sobie równe. Dolny lewy kąt razem z kątem między ramionami pierwszego trójkąta tworzą kąty przyległe a ich suma wynosi 180°. Skoro jeden z tych kątów ma miarę 180° – 2α, to drugi kąt musi mieć miarę 2α. Z kolei górny kąt w drugim trójkącie (między ramionami) stanowi razem z kątem 81° i wyznaczonym wcześniej kątem α kąty przyległe i razem dają 180°. Jego miara wynosi: 180° – 81° – α = 99° – α.
Kąty w trójkącie dają w sumie 180°. Więc sumując kąty w prawym trójkącie otrzymasz:
![]()
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
