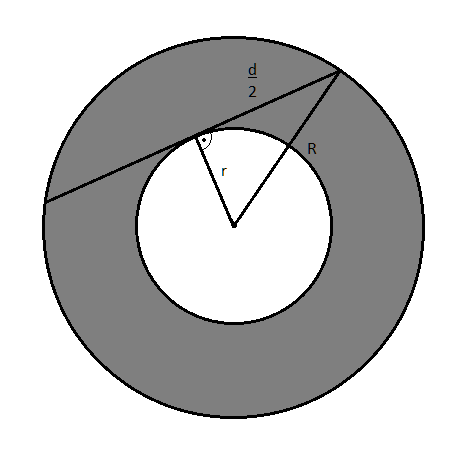
W tym zadaniu musisz obliczyć, ile wynosi pole zaznaczonego na poniższej ilustracji pierścienia, jeśli widoczna na niej cięciwa jest długości d i jest odcinkiem stycznym do wewnętrznego okręgu.
r – promień okręgu wewnętrznego
R – promień okręgu zewnętrznego
![]()
![]()
![]()
![]()
Odpowiedź: B. ![]()

Warto w tym zadaniu przerysować rysunek oraz zaznaczyć promienie okręgu wewnętrznego (r) oraz zewnętrznego (R).
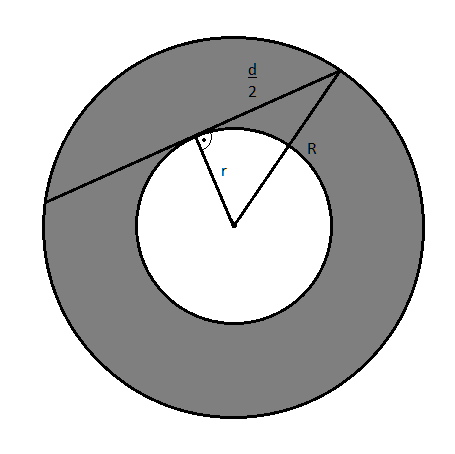
Pole zaznaczonego pierścienia to różnica pola okręgu zewnętrznego i wewnętrznego. Pole koła wyraża się wzorem P = πr2, wobec czego szukane pole pierścienia to będzie:
![]()
Musisz więc wyrazić R2 – r2 przez d.
Od środka okręgów możesz poprowadzić promień wewnętrznego okręgu do punktu styczności odcinka d z wewnętrznym okręgiem. Odcinek styczny do okręgu jest prostopadły do promienia poprowadzonego do punktu styczności, więc między promieniem wewnętrznym, a styczną jest kąt prosty. Styczna ta jest dzielona na dwie równe części. Ze środka okręgów możesz poprowadzić także promień zewnętrznego okręgu, do punktu na zewnętrznym okręgu, w którym styczna przecina się z zewnętrznym okręgiem. Otrzymujesz trójkąt prostokątny w którym przyprostokątnymi są r oraz połowa d, zaś przeciwprostokątną jest R. Z twierdzenia pitagorasa możesz zapisać:
![]()
Przenosząc r2 na drugą stronę otrzymasz szukane wyrażenie w zależności od d:
![]()
Podstawiając za to wyrażenie do wzoru na pole pierścienia otrzymasz:
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
