W tym zadaniu musisz wyznaczyć liczbę rozwiązań nierówności: ![]()
![]()
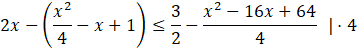
![]()
![]()
![]()
![]()
![]()
Odpowiedź: D. nieskończenie wiele

Aby określić, ile liczb naturalnych spełnia dane równanie musisz rozwiązać to równanie.
![]()
Pierwszym krokiem będzie skorzystanie ze wzoru skróconego mnożenia na kwadrat różnicy na nawiasach podniesionych do kwadratu.
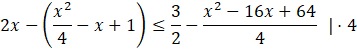
Następnie zauważ, że możesz pozbyć się ułamków w nierówności, przez przemnożenie obu stron przez 4.
![]()
Okazuje się, że wyrażenia z x2 upraszczają się i otrzymujesz zwykłą nierówność liniową.
![]()
Przenosisz więc niewiadome na jedną, a wiadome na drugą stronę.
![]()
Pozostaje już tylko podzielić obustronnie przez liczbę stojącą przy x.
![]()
Zauważ, że zastanawiamy się tutaj nad ilością liczb naturalnych spełniających tę nierówność, więc załóżmy, że x jest naturalny.
![]()
Pierwszą liczbą naturalną która spełnia tą nierówność jest 14, jednak wszystkie liczby naturalne spełniają tę nierówność. Więc jest nieskończona liczba naturalnych rozwiązań tej nierówności.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
