W tym zadaniu musisz sprawdzić, czy ziarna z próbki nowej odmiany grochu spełniają wymagania stawiane przed tą odmianą dotyczące wielkości i zróżnicowania. Stacja hodowli roślin prowadzi próby hodowli grochu, który ma mieć duże ziarna i niewielki rozrzut rozmiaru ziaren. Przyjęto, że średnio ziarna powinny ważyć więcej niż 0,06 g, zaś odchylenie standardowe masy ziaren nie powinno przekraczać 0,001 g. Przeprowadzono ważenie 100 ziaren tej nowej odmiany. Załączona tabela przedstawia wyniki uzyskane w badaniu pobranej próbki.
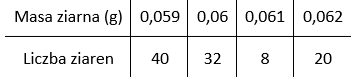
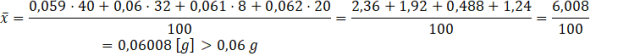
Wymagania spełnione.

Wymagania niespełnione.
Więc przebadane ziarna nie spełniają oczekiwań pod kątem odchylenia standardowego.

Aby określić, czy ziarna spełniają stawiane przed nimi oczekiwania musisz obliczyć średnią arytmetyczną oraz odchylenie standardowe ich mas.
Średnią arytmetyczną oblicz korzystając ze wzoru na nią. Oczywiście zamiast dodawać do siebie poszczególne masy kilkadziesiąt razy wystarczy, że je przemnożysz przez odpowiednią ilość ziaren. Pamiętaj, że wszystkich ziaren jest 100.
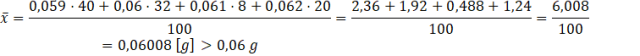
Więc oczekiwania co do średniej masy ziaren są spełnione.
Teraz oblicz odchylenie standardowe. Lepiej tutaj użyć drugiego wzoru na odchylenie standardowe. Podobnie jak w przypadku średniej, nie ma sensu dodawać kilkudziesięciu takich samych liczb, a wystarczy je przemnożyć przez ich ilość.

Z obliczeń wyszło, że odchylenie standardowe nie spełnia wymogu bycia mniejszym niż 0,001 g. Więc przebadane ziarna nie spełniają oczekiwań pod kątem odchylenia standardowego.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
