W tym zadaniu musisz wyznaczyć jaki wzór ma funkcja f(a) = b, czyli jak od wielkości a zależy b, jeśli dla dwóch prostokątów o wymiarach a x b oraz (a – 1) x b suma ich pól wynosi 10. W tym zadaniu musisz także wyznaczyć dziedzinę i zbiór wartości tej funkcji oraz naszkicować jej wykres.

Pole pierwszego prostokąta to po prostu ab, zaś pole drugiego to (a – 1)b. Suma tych pól ma wynosić zawsze 10.

$\text{[math]}$

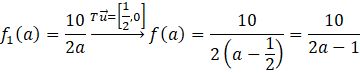
Wykresem funkcji f₁(a) będzie hiperbola o asymptotach x = 0 oraz y = 0.

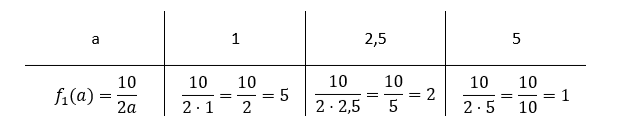
Na podstawie wykresu funkcji można odczytać, że zbiorem wartości funkcji f(a) jest:

$\text{[math]}$

Pole pierwszego prostokąta to po prostu ab, zaś pole drugiego to (a – 1)b. Suma tych pól ma wynosić zawsze 10.

$\text{[math]}$

Zauważ, że masz dwa składniki sumy, w których jest b. Więc możesz wyciągnąć b przed nawias.

$\text{[math]}$

Teraz aby uzyskać zależność b od a, wystarczy, że podzielisz obie strony przez nawias stojący przy b.

$\text{[math]}$

Zapisując to w postaci funkcji otrzymasz:

$\text{[math]}$

Gdyby to była zwykła funkcja, to jej dziedziną byłyby wszystkie liczby rzeczywiste poza tymi, które w mianowniku dają 0. Jednakże pamiętaj, że a i b to długości boków prostokątów, więc długości te nie mogą być ujemne. Ponieważ długość drugiego boku, to a – 1, to ta wartość także nie może być ujemna. Uwzględniając te informacje możesz obliczyć dziedzinę:

$\text{[math]}$

Zauważ, że dwie środkowe nierówności możesz zastąpić po prostu przez a > 1. Z kolei, jeśli chodzi o ostatnią nierówność, to zauważ, że jest to ułamek, którego licznik jest zawsze dodatni. Więc cały ułamek będzie dodatni jedynie, gdy mianownik będzie dodatni. Więc ostatnią nierówność możesz zastąpić przez 2a – 1 > 0.

$\text{[math]}$

Podsumowując te wszystkie nierówności otrzymujesz dziedzinę:

$\text{[math]}$

Zbiór wartości będzie łatwiej wyznaczyć dysponując wykresem.

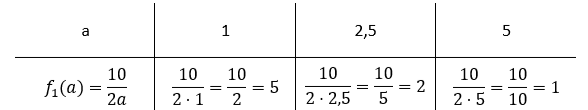
Otrzymana funkcja jest funkcją homograficzną, więc jej wykresem będzie hiperbola, a dokładniej jedno z jej ramion, gdyż dziedzina jest ograniczona. Aby ją narysować narysuj najpierw wykres funkcji $\text{[math]}$ , a następnie przesuń go o wektor $\text{[math]}$ tak by otrzymać wykres funkcji, którą masz narysować. Funkcję trzeba przesunąć o ten wektor, gdyż wtedy wykres funkcji po przesunięcie będzie opisany wzorem $\text{[math]}$ . Z kolei wykresem funkcji f₁(a) będzie po prostu hiperbola. Aby ją narysować zaznacz asymptoty na osiach układu współrzędnych oraz wybierz trzy dodatnie argumenty i oblicz wartości funkcji f₁(a) dla nich, aby narysować ramię dodatnie tej hiperboli. Możesz zapisać to za pomocą tabelki:

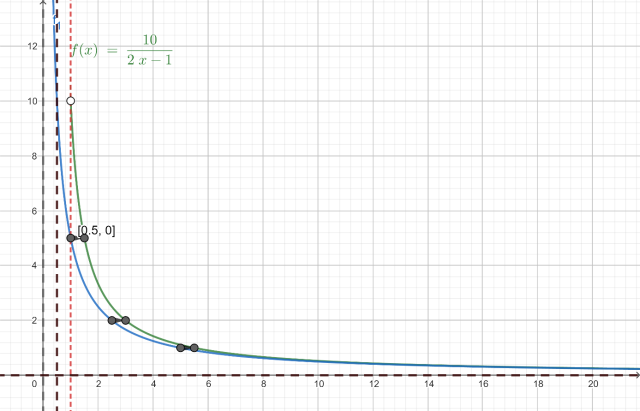
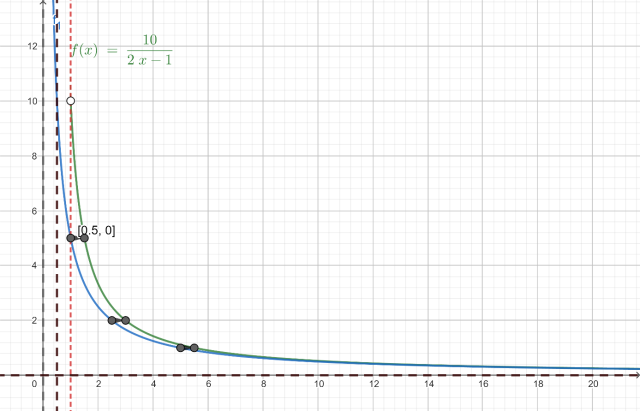
Teraz, po zaznaczeniu tych punktów, możesz narysować funkcję f₁(a), a następnie przesunąć ją o wektor $\text{[math]}$ oraz zaznaczyć dziedzinę, aby uzyskać wykres funkcji f(a).

Główna funkcja zaznaczona jest na zielono, funkcja f₁(a) jest zaznaczona na niebiesko, czerwona przerywana linia to początek dziedziny, szara pionowa przerywana linia to asymptota funkcji f₁(a), zaś czarne przerywane linie to asymptoty funkcji f(a).

Matematyka z Plusem. Klasa 4. Podręcznik – rozwiązania i odpowiedzi

Zadanie 16. - strona 111

Zadanie

Rozwiązanie

Wyjaśnienie

Matematyka - wybrane pytania