W tym zadaniu musisz określić który spośród wymienionych ciągów jest rosnący.
A. ![]()
![]()
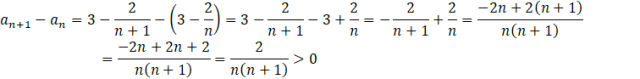
Ciąg jest rosnący.
B. ![]()
![]()
![]()
Ciąg jest rosnący.
C. ![]()
![]()
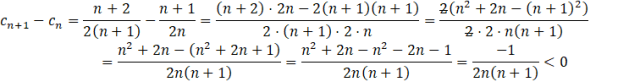
Ciąg jest malejący.
D. ![]()
![]()
![]()
Większe lub mniejsze od zera w zależności od n, więc ciąg nie jest monotoniczny
Odpowiedź: A. ![]()
![]()

Aby określić który z podanych ciągów jest rosnący musisz sprawdzić monotoniczność każdego ciągu. Monotoniczność sprawdzasz, przez obliczenie wyrazu następnego (a więc n+1) lub ewentualnie poprzedniego (n-1) i sprawdzenie czy różnica an+1 – an jest dodatnia czy ujemna (w przypadku wzięcia wyrazu poprzedniego, to sprawdzasz różnicę an – an-1, po prostu od wyrazu kolejnego odejmujesz wyraz poprzedni)
E. ![]()
![]()
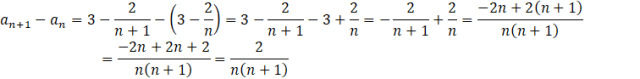
Na ogół, gdy pojawia się różnica lub suma ułamków, to warto je sprowadzić do wspólnego mianownika. Otrzymane wyrażenie musisz oszacować, czy jest dodatnie czy ujemne. Pamiętaj, że n jest liczbą naturalną, a więc jest zawsze dodatnie. W mianowniku zawsze jest mnożenie dwóch liczb naturalnych (bo dodając 1 do liczby naturalnej i tak otrzymasz liczbę naturalną). Oznacz to, że mianownik ułamka będzie zawsze dodatni. W liczniku jest 2, czyli liczba dodatnia. Po podzieleniu liczby dodatniej, przez dodatnią otrzymasz liczbę dodatnią. Oznacza to, że gdy od wyrazu następnego odejmiesz poprzedni, to dostaniesz coś dodatniego. Więc wyraz następny jest większy od poprzedniego, a więc ten ciąg jest rosnący.
F. ![]()
![]()
![]()
Otrzymane wyrażenie musisz oszacować, czy jest dodatnie czy ujemne. Pamiętaj, że n jest liczbą naturalną, a więc jest zawsze dodatnie. Dla n = 1, to wyrażenie będzie dodatnie (bo 2 + 1 = 1). Dla większych n tym bardziej to wyrażenie będzie dodatnie. Więc, gdy od wyrazu następnego odejmiesz poprzedni, to dostaniesz coś dodatniego, czyli wyraz poprzedni jest mniejszy od następnego, a więc ten ciąg jest rosnący.
G. ![]()
![]()
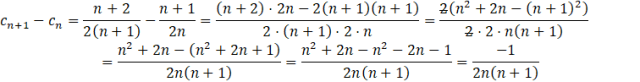
Podobnie jak w odpowiedzi A., gdy pojawia się różnica lub suma ułamków, to warto je sprowadzić do wspólnego mianownika. Warto nie wymnażać nawiasów przez 2, tylko wyciągnąć 2 przed nawias i skrócić. Otrzymane wyrażenie musisz oszacować, czy jest dodatnie czy ujemne. Pamiętaj, że n jest liczbą naturalną, a więc jest zawsze dodatnie. W mianowniku zawsze jest mnożenie dwóch liczb naturalnych (bo dodając 1 do liczby naturalnej i tak otrzymasz liczbę naturalną). Oznacz to, że mianownik ułamka będzie zawsze dodatni. Ale w liczniku jest -1, czyli liczba ujemna. Po podzieleniu liczby ujemnej, przez dodatnią otrzymasz liczbę ujemną. Oznacza to, że gdy od wyrazu następnego odejmiesz poprzedni, to dostaniesz coś ujemnego. Więc wyraz poprzedni jest większy od następnego, a więc ten ciąg jest malejący.
H. ![]()
![]()
![]()
Ponieważ otrzymałeś tutaj różnicę wartości bezwzględnych, to nie możesz jednoznacznie określić jaki znak będzie miał wynik tego odejmowania. Ale zauważ, że oba moduły różnią się jedynie liczbą, od której odejmuje się n. Dla małych n (mniejszych od 6), większą wartość otrzymasz w drugim module, a więc wynik będzie ujemny. Ale gdy weźmiesz n większe od 6 (np. 10), to większa liczba będzie pod pierwszą wartością bezwzględną, a więc wynik wyjdzie dodatni. Oznacza to, że ten ciąg jest malejący do pewnego momentu (n=6), a dalej jest rosnący. Taki ciąg nie jest w ogóle monotoniczny, a tym bardziej rosnący.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
