W tym zadaniu musisz określić czy funkcja h(x) jest monotoniczna, jeśli ta funkcja jest zdefiniowana jako h(x) = f(x) – g(x) oraz wykresy funkcji f(x) i g(x) są na rysunku.
Dla funkcji f(x) i g(x) prawdziwe są implikacje:
![]()
![]()
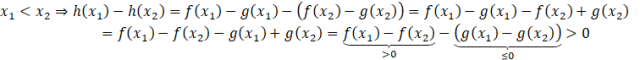
![]()
Odp.: Funkcja h(x) jest malejąca, czyli monotoniczna.

Zauważ, że funkcja f(x) jest malejąca w całym określonym przedziale, zaś funkcja g(x) jest niemalejąca w całej dziedzinie.
Dla tych funkcji prawdziwe są implikacje:
![]()
![]()
Druga implikacja wynika z tego, że funkcja g(x) jest niemalejąca, a więc jest rosnąca lub stała.
Dla ułatwienia zadania przenieś wszystkie składniki na jedną stronę:
![]()
![]()
Teraz musisz na podstawie tych dwóch nierówności rozważyć różnicę h(x1) – h(x2) dla x1
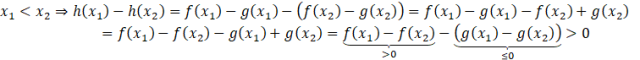
Najpierw korzystając ze wzoru funkcji h(x) podstawiasz odpowiednie wyrażenia, następnie grupujesz je tak, aby dostać wyrażenia których wartość znasz na podstawie własności funkcji f(x) i g(x) (implikacje wyżej). Ponieważ dostałeś ![]()
![]()
Przenosząc h(x2) na drugą stronę otrzymasz:
![]()
A więc funkcja h(x) jest malejąca, czyli monotoniczna.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
