W tym zadaniu musisz obliczyć dla jakiej najmniejszej ilości elementów ciągu arytmetycznego ich suma będzie większa od 100 wiedząc, że wyraz trzynasty tego ciągu wynosi 0, zaś dwudziesty trzeci to 2.

Wzór ogólny rozważanego ciągu:

$\text{[math]}$

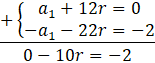
Więc wzór na n-ty wyraz tego ciągu wygląda następująco:

$\text{[math]}$

Gdzie S_n to suma rozważanego ciągu. Wyraża się ona wzorem:

$\text{[math]}$

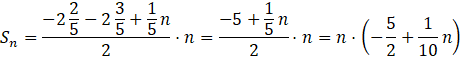
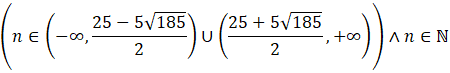
Odp.: Aby suma tego ciągu była większa od 100 należy dodać przynajmniej 47 wyrazów tego ciągu.

W pierwszej kolejności musisz wyznaczyć wzór ogólny tego ciągu. Aby to zrobić, przypomnij sobie jak wygląda wzór na n-ty wyraz ciągu arytmetycznego:

$\text{[math]}$

A następnie zapisz w taki sposób znane wyrazy:

$\text{[math]}$

Ułóż z dwóch otrzymanych wzorów układ równań:

$\text{[math]}$

Ponieważ w obu równaniach przy a₁ jest ten sam współczynnik, to najszybciej ten układ równań rozwiążesz z metody przeciwnych współczynników. Aby wykorzystać tę metodę, to przemnóż którekolwiek równanie przez -1, a następnie dodaj je stronami.

$\text{[math]}$

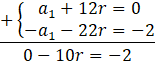
Aby uzyskać a₁ podstaw otrzymany wynik do któregokolwiek z wcześniejszych równań.

$\text{[math]}$

Więc wzór na n-ty wyraz tego ciągu wygląda następująco:

$\text{[math]}$

Aby policzyć powyżej ilu wyrazów tego ciągu, ich suma będzie większa od 100, musisz rozwiązać nierówność:

$\text{[math]}$

Gdzie S_n to suma tego ciągu. Wyraża się ona wzorem:

$\text{[math]}$

Podstawiając znane wartości otrzymasz:

$\text{[math]}$

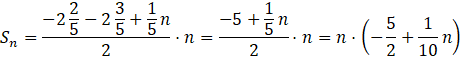
Teraz musisz wrócić do głównej nierówności:

$\text{[math]}$

Wymnóż nawias i przenieś wszystkie wyrazy na lewą stronę. Aby rozwiązać tę nierówność, będziesz musiał obliczyć miejsca zerowe tej funkcji i narysować wykres.

$\text{[math]}$

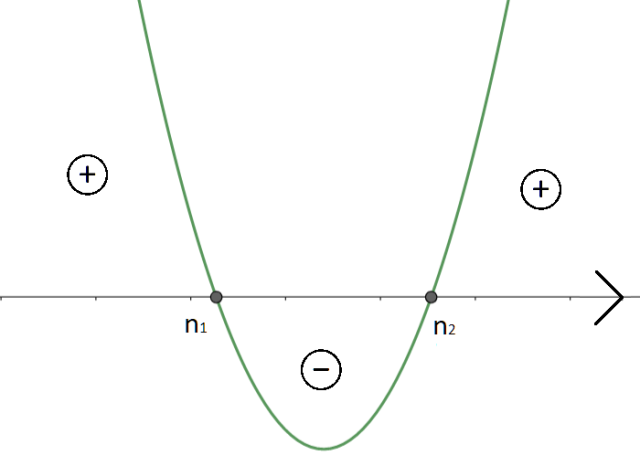
Teraz musisz naszkicować orientacyjny wykres tej funkcji. Współczynnik a jest dodatni, więc ramiona paraboli będą zwrócone ku górze. Nie ma sensu przepisywać całych wyrażeń, które są miejscami zerowymi, a wystarczy, że opiszesz je jako n₁ i n₂. Ten wykres jest tylko wykresem orientacyjnym.

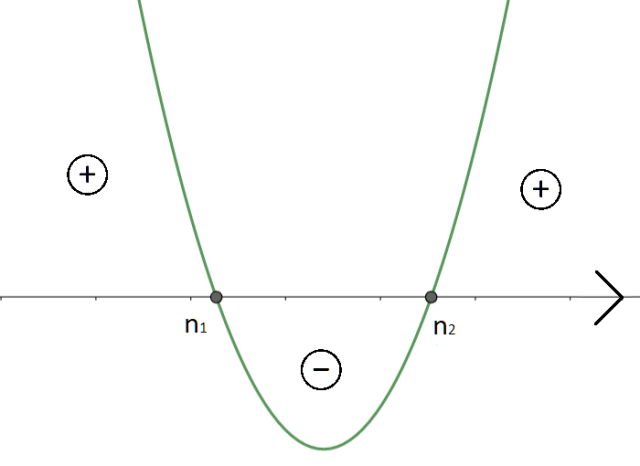
Ponieważ, w nierówności funkcja ma być większa od zera, to rozwiązaniem tej nierówności są te przedziały, dla których funkcja jest dodatnia. Pamiętaj, że w tym przypadku nie uwzględniasz miejsc zerowych.

$\text{[math]}$

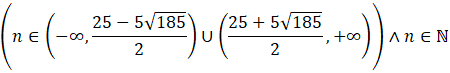
Musisz uwzględnić, że n to numer indeksu, więc jest to liczba naturalna. Więc wszystkie liczby naturalne które spełniają tę nierówność to:

Matematyka z Plusem. Klasa 4. Podręcznik – rozwiązania i odpowiedzi

Zadanie 23. - strona 108

Zadanie

W tym zadaniu musisz obliczyć dla jakiej najmniejszej ilości elementów ciągu arytmetycznego ich suma będzie większa od 100 wiedząc, że wyraz trzynasty tego ciągu wynosi 0, zaś dwudziesty trzeci to 2.

Rozwiązanie

Wyjaśnienie

Matematyka - wybrane pytania