W tym zadaniu musisz określić jaki jest zbiór wartości funkcji g(x) = f(x + 50) – 20, jeśli funkcja f(x) jest definiowana jako:
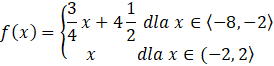
![]()
![]()
![]()
Zbiorem wartości funkcji z pierwszego wzoru jest zbiór: ![]()
Zbiorem wartości funkcji z drugiego wzoru jest zbiór ![]()
![]()
![]()
![]()
![]()
Odpowiedź: A. ![]()

Zauważ, że funkcja g(x) powstaje przez przesunięcie funkcji f(x) o wektor [-50, -20] co możesz zapisać jako:
![]()
Oznacza to, że jeśli obliczysz zbiór wartości funkcji f(x), to aby otrzymać zbiór wartości g(x) od krańców tak otrzymanego przedziału będziesz musiał odjąć 20 (gdyż ujemna druga współrzędna wektora, o który przesuwa się funkcję odpowiada przesunięciu funkcji w dół).
Oba wzory wykorzystywane we wzorze na f(x) są wzorami na funkcje liniowe, więc ich największa i najmniejsza wartość jest na końcach przedziałów, na których są określane. Więc wystarczy obliczyć wartości tych funkcji na końcach przedziałów:
![]()
![]()
Zbiorem wartości funkcji z pierwszego wzoru jest zbiór: ![]()
Zbiorem wartości funkcji z drugiego wzoru jest zbiór ![]()
Gdy zsumujesz te dwa zbiory otrzymasz zbiór wartości tej funkcji:
![]()
Aby otrzymać zbiór wartości funkcji g(x) tak jak to już zostało wspomniane musisz od obu krańców przedziałów odjąć 20.
![]()
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
