W tym zadaniu musisz obliczyć jak długi jest odcinek a zaznaczony na poniższej ilustracji.
Z twierdzenia Pitagorasa zastosowanego do małego trójkąta:
![]()
![]()
Gdzie b – przeciwprostokątna małego trójkąta ale także przyprostokątna dużego trójkąta
Z twierdzenia Pitagorasa zastosowanego do dużego trójkąta:
![]()
![]()
![]()
Z twierdzenia Pitagorasa zastosowanego do średniego trójkąta:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
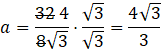
Odpowiedź: A. ![]()

Zauważ, że zaznaczony odcinek a jest przyprostokątną w małym, prawym trójkącie. Drugą przyprostokątną jest odcinek o długości 4. Wobec czego długość przeciwprostokątnej tego trójkąta (b) możesz obliczyć z twierdzenia Pitagorasa i wynosi ona:
![]()
![]()
Zauważ, że odcinek b, jest przyprostokątną dużego trójkąta, który także jest prostokątny. Jego drugą przyprostokątną jest odcinek o długości 8. Wobec czego długość przeciwprostokątnej tego trójkąta (c) także możesz obliczyć z twierdzenia Pitagorasa i wynosi ona:
![]()
![]()
![]()
Na rysunku jest jeszcze jeden trójkąt prostokątny. Jest to mały trójkąt z lewej strony. Jego przyprostokątną jest odcinek o długości 4, zaś przeciwprostokątną – odcinek o długości 8. Długość drugiej przeciwprostokątnej (d) wylicz z twierdzenia Pitagorasa i wynosi ona:
![]()
![]()
![]()
![]()
Oczywiście długość ta nie może być ujemna i odrzucasz od razu ujemny przypadek.
Zauważ, że odcinek c składa się z odcinków a oraz d.
![]()
Podstawiając wyliczone wcześniej wartości otrzymasz:
![]()
Aby pozbyć się pierwiastka z prawej strony musisz podnieść obie strony do kwadratu. Z prawej strony zastosuj wzór skróconego mnożenia na kwadrat sumy.
![]()
![]()
![]()
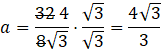
Ponieważ w mianowniku jest pierwiastek musisz usunąć niewymierność, przez przemnożenie licznika i mianownika przez ten pierwiastek.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
