W tym zadaniu musisz wyznaczyć jakim równaniem będzie opisana prosta stykająca się z okręgiem zadanym równaniem (x + 2)2 + (y – 1)2 = 5 w punkcie (1, 3).
Szukane współrzędne końców cięciwy to punkty przecięcia podanej prostej z okręgiem.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Więc współrzędne końców cięciwy podanego okręgu wyciętej przez podaną prostą to:
![]()
![]()

Szukane współrzędne końców cięciwy to po prostu punkty przecięcia podanej prostej z okręgiem. Aby je znaleźć musisz rozwiązać układ równań składający się z równań prostej i okręgu.
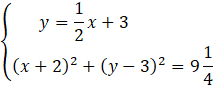
Zauważ, że z pierwszego równania masz od razu wyznaczonego y w zależności od x, więc podstaw do równania okręgu równanie prostej.
![]()
![]()
Do nawiasu zastosuj wzór skróconego mnożenia.
![]()
Pomnóż obie strony równania przez 4, aby pozbyć się ułamków.
![]()
Uprość wyrażenie i przenieś wszystkie wyrazy na jedną stronę:
![]()
Otrzymałeś równanie kwadratowe. Aby je rozwiązać musisz policzyć Δ.
![]()
![]()
![]()
![]()
Aby wyznaczyć drugie współrzędne tych punktów wystarczy, że podstawisz otrzymane wartości x do któregokolwiek równania. Oczywiście zdecydowanie łatwiej jest podstawić je do równania prostej.
![]()
![]()
Więc współrzędne końców cięciwy podanego okręgu wyciętej przez podaną prostą to:
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
