W tym zadaniu musisz określić, ile wynosi pole trójkąta ograniczonego prostymi y = 2x, ![]()
Punkt A (przecięcie się prostej ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Punkt B (przecięcie się prostej ![]()
x = 0
![]()
![]()
![]()
Punkt O (przecięcie się prostej ![]()
x = 0
![]()
![]()
Bok OB ma długość 7 (gdyż oba punkty są na osi OY, więc wystarczy odjąć od siebie drugie współrzędne).
Równanie osi OY w postaci ogólnej ma postać x = 0
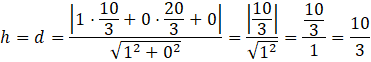
Pole trójkąta ABO wynosi:
![]()
Odpowiedź: A. ![]()

Aby obliczyć pole tego trójkąta musisz znaleźć długość jego jednego boku oraz wysokość na niego opuszczoną. Wysokość, to nic innego jak odległość przeciwnego do danego boku wierzchołka od prostej w której zawiera się dany bok. Niezależnie od tego który bok i wysokość wybierzesz, musisz obliczyć współrzędne wierzchołków tego trójkąta. Współrzędne te to punkty przecięć się prostych zawierających boki trójkąta ze sobą. Dwie proste w punkcie przecięcia się mają tę samą wartość, więc wystarczy przyrównać do siebie ich równania. Aby otrzymać drugą współrzędną danego punktu musisz podstawić otrzymaną wartość x do któregokolwiek równania. Oś OY to prosta o równaniu x = 0.
Punkt A (przecięcie się prostej ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Punkt B (przecięcie się prostej ![]()
![]()
![]()
![]()
Punkt O (przecięcie się prostej ![]()
![]()
![]()
Wybierz bok OB i na jego podstawie oblicz pole tego trójkąta (ale w zasadzie jest dowolne który bok wybierzesz).
Bok OB ma długość 7 (gdyż oba punkty są na osi OY, więc wystarczy odjąć od siebie drugie współrzędne). Aby obliczyć długość wysokości opuszczonej na ten bok z punktu A skorzystaj ze wzoru na odległość punktu od prostej. Równanie osi OY w postaci ogólnej ma także postać x = 0, więc współczynnik A wynosi 1, zaś B oraz C wynoszą 0. Podstawiając te współczynniki oraz współrzędne punktu A otrzymasz:
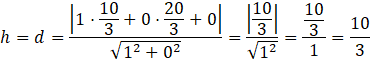
Pole tego trójkąta wynosi:
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
