W tym zadaniu musisz policzyć jaki jest obwód równoległoboku, którego dłuższa przekątna o długości 5 rozdziela kąt tego równoległoboku na dwa kąty o miarach 20° i 40°.
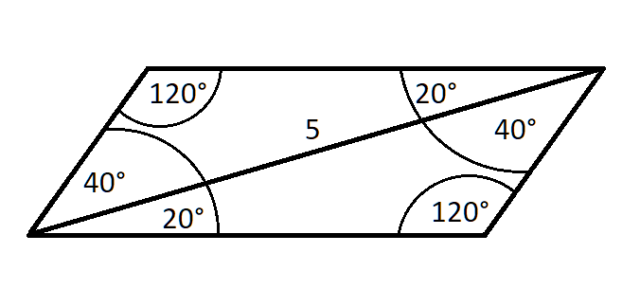
Miara kąta ostrego: 20° + 40° = 60°
Miara kąta rozwartego: 180° – 60° = 120°
Ponieważ kąty powstałe przez przedzielenie przeciwnego kąta ostrego są kątami naprzeciwległymi to mają takie wartości jak na rysunku.
Z twierdzenia sinusów:
![]()
Gdzie a i b to są boki tego równoległoboku.
![]()
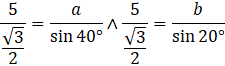
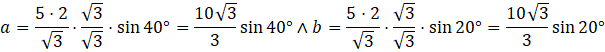
![]()
![]()

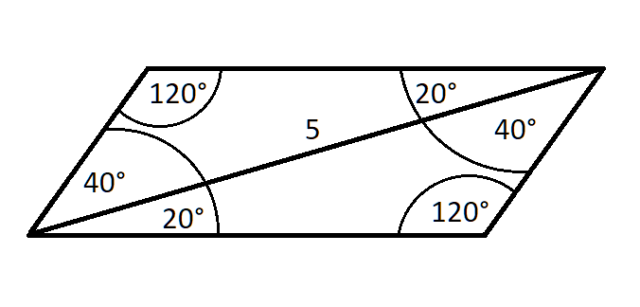
Skoro przekątna dzieli kąt na kąty 20° oraz 40° to kąt ten ma łącznie 60°. Suma kątów przy jednym ramieniu w równoległoboku wynosi 180°, więc drugi kąt tego równoległoboku wynosi 180° – 60° = 120°. Taką samą wartość ma również drugi kąt rozwarty. Zauważ, że przekątna leży na prostej przeciętej przez dwie równoległe proste, które zawierają dwa boki równoległoboku. Więc kąty przy przekątnej i jednym boku oraz kąty przy przekątnej i drugim boku są kątami naprzeciwległymi. Mając wszystkie wartości kątów możesz przejść do wyznaczania długości boków.
Z twierdzenia sinusów możesz zapisać, że:
![]()
Gdzie a i b to są boki tego równoległoboku.
Ponieważ wartość sin 120° nie znajduje się w żadnej tabelce, musisz obliczyć jego wartość. Użyj do tego wzorów redukcyjnych. Skorzystaj tutaj z tego, że:
![]()
Kąt 120° możesz zapisać jako 180° – 60°, więc kątem α ze wzoru będzie 60°.
![]()
Zapisz twierdzenie sinusów jako dwa wzory, każdy osobno dla jednego boku.
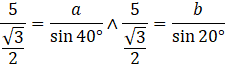
Przemnóż każde równanie przez wartość mianownika ze zmienną, tak aby pozbyć się tego mianownika.
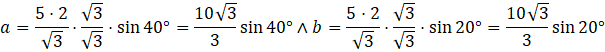
Aby obliczyć obwód równoległoboku wystarczy, że długość każdego z boków przemnożysz przez 2 i dodasz do siebie.
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
