W tym zadaniu musisz wyznaczyć dziedzinę funkcji f(x) = logx(x + 1)(x – 7).
![]()
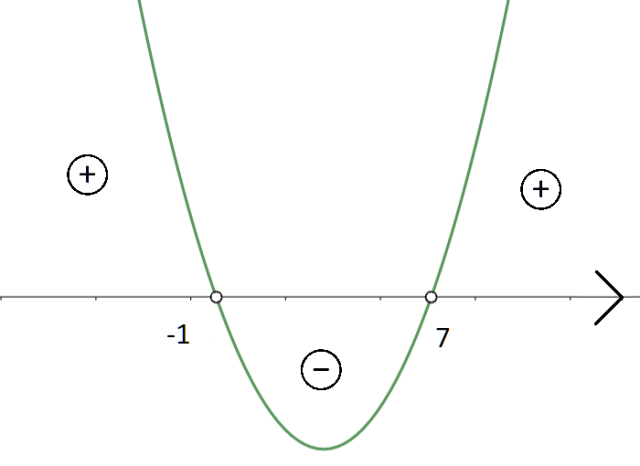
Wyrażenie po lewej stronie nierówności będzie dodatnie dla ![]()
![]()
![]()
Odpowiedź: A. ![]()

Skorzystaj tutaj z założeń w definicji logarytmu. Podstawa logarytmu musi być większa od 0 i różna od 1, zaś liczba logarytmowana musi być większa od 0. Wykorzystaj te informacje i napisz odpowiednie nierówności z podstawą i liczbą logarytmowaną logarytmu ze wzoru funkcji.
![]()
Skup się teraz na ostatniej nierówności. Zauważ, że jest to nierówność kwadratowa, a funkcja kwadratowa w niej występująca jest zapisana w postaci iloczynowej. Możesz natychmiast odczytać miejsca zerowe tej funkcji i wynoszą one -1 oraz 7 (pamiętaj o zmianie znaku przy odczytywaniu miejsc zerowych z postaci iloczynowej funkcji kwadratowej). Musisz narysować wykres tej funkcji kwadratowej. Ponieważ współczynnik przy najwyższej potędze jest dodatni (a w wzorze funkcji kwadratowej) to ramiona paraboli będą skierowane ku górze.
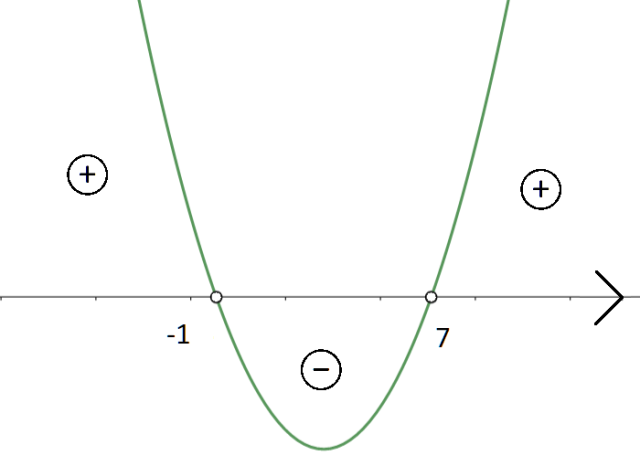
Jak możesz odczytać z wykresu, wyrażenie po lewej stronie nierówności będzie dodatnie dla ![]()
![]()
Co się sprowadza do:
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
