W tym zadaniu musisz wyznaczyć wartość wyrażenia sin α∙ cos α wiedząc, że prawdziwe jest wyrażenie ![]()
![]()
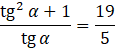
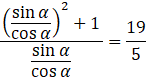
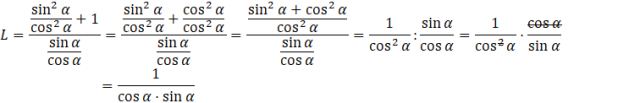
![]()
![]()
![]()
Odpowiedź: C. ![]()

Przypomnij sobie zależność wiążącą ze sobą tangensa, sinusa i cosinusa danego kąta. Tangens wyraża się jako iloraz sinusa i cosinusa danego kąta. Więc możesz zapisać:
![]()
Jednak zanim podstawisz do podanego wyrażenia, to przekształć je, aby łatwiej było działać na nim. Sprowadź je do wspólnego mianownika oraz zamień liczbę mieszaną na ułamek niewłaściwy.
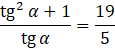
Teraz podstaw wyrażenie z sinusem i cosinusem.
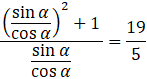
Skup się na lewej stronie równania. Podnieś do kwadratu nawias, a następnie sprowadź licznik do wspólnego mianownika. Zauważ, że licznik ułamku w liczniku to jedynka trygonometryczna. Zapisz kreskę ułamkową jako dzielenie, a następnie skorzystaj z tego, że dzieląc przez ułamek mnożysz przez jego odwrotność. Możesz skrócić cosinusy i otrzymujesz szukane wyrażenie w mianowniku lewej strony.
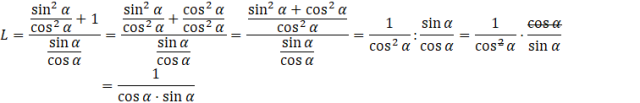
Wróć do równania wstawiając lewą stronę po przekształceniach:
![]()
Po obu stronach równania są ułamki, więc możesz wymnożyć to równanie „na krzyż”.
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
