W tym zadaniu musisz obliczyć, ile wynoszą zmienne p i q, jeśli 7 = 3b, logp q = b – 2 i 3pq = 7.
D: p>0 ∧ p≠1 ∧ q>0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Z własności logarytmów można stwierdzić, że p=3
![]()
![]()
![]()
![]()
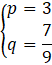

Na samym początku, ponieważ zmienne p i q są odpowiednio podstawą i liczbą logarytmowaną, musisz wyznaczyć dziedzinę. Zarówno podstawa jak i liczba logarytmowana muszą być dodatnie, ponadto, podstawa nie może wynosić 0.
D: p>0 ∧ p≠1 ∧ q>0
W kolejnym kroku wyznaczasz b z definicji logarytmu. Logarytm to wykładnik do jakiego musisz podnieść podstawę, aby uzyskać liczbę logarytmowaną. Tutaj, aby uzyskać 7, musisz 3 podnieść do potęgi b, więc można to zapisać w postaci logarytmu o podstawie 3 z 7.
![]()
W dalszym kroku z ostatniego równania wyznaczasz q. Dlaczego akurat q? Spójrz na środkowe równanie. Zmienna p jest w podstawie logarytmu. Zdecydowanie łatwiej jest przeprowadzać obliczenia, jeśli podstawa jest stosunkowo prosta. Zadanie by się utrudniło, gdyby w podstawie dać za p ułamek z q.
![]()
![]()
Po wyznaczeniu q możesz podstawić otrzymane wyrażenie do drugiego równania.
![]()
Aby dostać równanie logarytmiczne, zamień prawą stronę na logarytm o tej samej podstawie co lewa strona, a więc p. Robisz to przez napisanie logarytmu o podstawie p z p podniesionego do potęgi takiej, jaka tam wcześnie stała.
![]()
Otrzymujesz równanie logarytmiczne więc możesz opuścić logarytmy.
![]()
Podstaw za b wcześniej wyliczony logarytm oraz pozbądź się p z lewej strony.
![]()
![]()
Aby prawą stronę zapisać za pomocą jednej potęgi, wykonaj podstawowe działania na potęgach. Samo p jest w potędze o wykładniku 1, zaś jeśli mnożysz potęgi o tych samych podstawach, to dodajesz ich wykładniki.
![]()
![]()
Przejdź do otrzymanego wykładnika. Zauważ, że masz tam różnicę logarytmu i 1. Warto zapisać 1 jako logarytm o podstawie 3, aby móc skorzystać ze wzoru na różnicę logarytmów.
![]()
Różnica logarytmów to logarytm ilorazu.
![]()
Po skorzystaniu z tego wzoru otrzymujesz p do potęgi logarytmu o podstawie 3. Zauważ, że to co jest logarytmowane w wykładniku, jest po lewej stronie równania. Przypomnij sobie własność logarytmów taką, że jeśli liczbę podniesiesz do potęgi logarytmu takiej samej podstawie to otrzymasz jedynie liczbę logarytmowaną. Tutaj mamy do czynienia z właśnie taką sytuacją. Więc jedyną opcją jest, że p wynosi 3. Oczywiście musisz sprawdzić, czy zawiera się w dziedzinie.
![]()
W ostatnim kroku, pozostaje wyznaczyć q na podstawie wcześniej uzyskanej zależności i sprawdzić, czy q także zawiera się w dziedzinie.
![]()
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
