W tym zadaniu musisz obliczyć, ile wynosi pole zaznaczonego na rysunku obok trójkąta.
Pole dużego trójkąta:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Z twierdzenia Pitagorasa zastosowanego dla zamalowanego trójkąta:
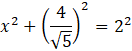
![]()
![]()

Pole zacieniowanego trójkąta:
![]()
![]()
Odpowiedź: C. ![]()

W pierwszej kolejności oblicz pole dużego trójkąta. W trójkącie prostokątnym pole obliczysz mnożąc przyprostokątne i dzieląc wynik przez 2 (jedną z przyprostokątnych możesz potraktować jako bok, zaś drugą jako wysokość).
![]()
Następnie oblicz z twierdzenia Pitagorasa długość przeciwprostokątnej dużego trójkąta.
![]()
![]()
![]()
![]()
Oczywiście przeciwprostokątna musi być dodatnia, więc od razu możesz odrzucić ujemny przypadek.
Mając długość przeciwprostokątnej oraz pole możesz obliczyć wysokość dużego trójkąta opuszczoną na przeciwprostokątną (h).
Pole tego trójkąta wyraża się także jako:
![]()
Podstawiając znane wartości pola oraz przeciwprostokątnej obliczysz wysokość.
![]()
![]()
Ponieważ wysokość ta będzie później używana nie musisz usuwać niewymierności z mianownika.
Zauważ, że otrzymana wysokość, jest przyprostokątną zaznaczonego trójkąta. A ponieważ podana jest także przeciwprostokątna tego trójkąta (2) możesz zapisać twierdzenie Pitagorasa dla tego trójkąta (gdyż jest on także trójkątem prostokątnym).
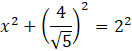
![]()
![]()
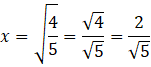
Oczywiście od razu możesz odrzucić ujemny przypadek. Podobnie jak w przypadku wysokości, nie musisz usuwać niewymierności z mianownika, gdyż nie jest to jeszcze końcowy wynik.
Pole zacieniowanego trójkąta to po prostu:
![]()
![]()

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
