W tym zadaniu musisz obliczyć, ile wynoszą miejsca zerowe funkcji: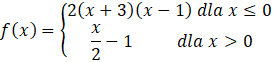
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A więc miejsca zerowe funkcji f to -3 oraz 2.
Odpowiedź: C. -3 i 2.

Aby wyliczyć miejsca zerowe funkcji w takiej postaci, musisz wyliczyć miejsca zerowe funkcji składowych a następnie sprawdzić, czy te miejsca zerowe mieszczą się w przedziale, dla którego określony jest dany wzór. Pamiętaj, że miejsca zerowe to argumenty funkcji dla których wartość funkcji wynosi 0. Więc obliczenie miejsc zerowych będzie polegało na przyrównaniu funkcji do 0.
Zauważ, że pierwszy wzór, to funkcja kwadratowa w postaci iloczynowej. Aby obliczyć jej miejsca zerowe wystarczy przyrównać każdy z nawiasów do 0. (Gdyż, gdy przyrównasz iloczyn do 0, to któryś z jego składników musi być zerem).
![]()
![]()
![]()
Teraz musisz sprawdzić, czy te rozwiązania należą do przedziału, w którym obowiązuje ten wzór.
![]()
Analogicznie postępujesz z drugim wzorem, który jest zwykłą funkcją liniową:
![]()
![]()
![]()
![]()
A więc miejsca zerowe funkcji f to -3 oraz 2.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
