W tym zadaniu musisz obliczyć jaka jest długość wysokości rombu, którego przekątne mają długości 3 oraz 8.
![]()
Gdzie, e oraz f to są długości przekątnych
![]()
![]()
Z twierdzenia Pitagorasa:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
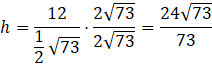
Odpowiedź: D. ![]()

Znając długości dwóch przekątnych rombu jesteś w stanie obliczyć jego pole.
![]()
Gdzie, e oraz f to są długości przekątnych. Podstawiając podane długości otrzymasz:
![]()
Pole rombu możesz też obliczyć ze wzoru wykorzystującego długość boku oraz wysokość rombu:
![]()
Więc gdybyś znał długość boku rombu mógłbyś obliczyć wysokość. Zauważ, że przekątne w rombie przecinają się dokładnie w połowie i dokładnie pod kątem prostym. Więc połowy przekątnych oraz bok rombu tworzą trójkąt prostokątny, w którym bok rombu jest przeciwprostokątną. Znając długości przyprostokątnych (czyli połowy przekątnych rombu) możesz obliczyć przeciwprostokątną (czyli bok rombu) korzystając z twierdzenia Pitagorasa. Długość boku rombu konsekwentnie będzie oznaczana jako a.
![]()
![]()
![]()
![]()
Oczywiście długość boku nie może być ujemna, więc od razu możesz odrzucić ujemny przypadek.
![]()
Aby uprościć ten pierwiastek podziel 18,25 przez 0,25. W ten sposób otrzymasz liczbę, która po przemnożeniu przez 0,25 da 18,25 i uda ci się zapisać pierwiastkowaną liczbę jako iloczyn ułamka, którego pierwiastek możesz łatwo policzyć oraz liczby całkowitej.
Znając długość boku oraz pole rombu możesz obliczyć jego wysokość przez podstawienie znanych wartości do wzoru na pole rombu.
![]()
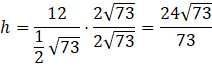
Ponieważ w mianowniku jest pierwiastek musisz go usunąć stamtąd przez pomnożenie licznika i mianownika przez ten pierwiastek. Warto jeszcze przemnożyć licznik i mianownik przez 2, aby pozbyć się ułamka z mianownika.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
