W tym zadaniu musisz udowodnić, że jeśli trapez ABCD ma ramię BC o tej samej długości co krótsza podstawa CD, to przekątną łącząca wierzchołki B i D jest dwusieczną kąta ABC.
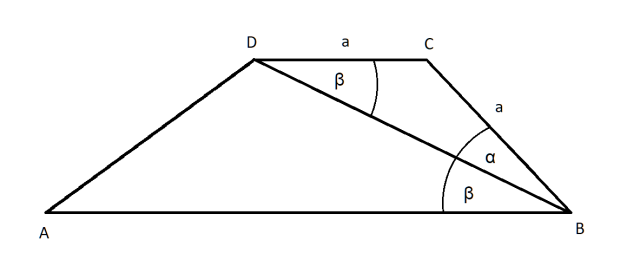
|∢ABD| = β
|∢DBC| = α
Kąty ABD oraz BDC – kąty naprzeciwległe, gdyż odcinki AB i CD są równoległe (podstawy trapezu). Więc |∢ABD| = |∢BDC| = β.
Trójkąt BCD – trójkąt równoramienny, gdzie ramionami są odcinki BC i CD, które są sobie równe z treści zadania.
Kąty DBC i BDC – kąty przy podstawie trójkąta równoramiennego, więc |∢DBC| = |∢BDC|. Wobec czego α = β, czyli |∢ABD| = |∢DBC|, co należało dowieść.

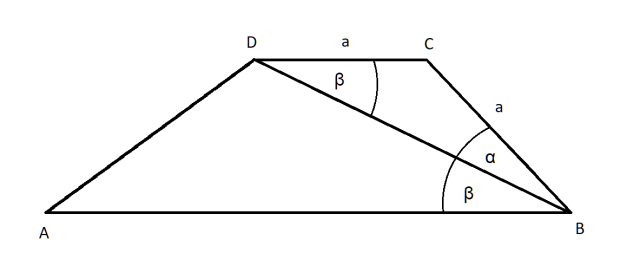
Oznacz kąty powstałe przez podział kąta ABC przez przekątną BD jako α i β. Zauważ, że kąt ABD oraz kąt BDC są kątami naprzeciwległymi, gdyż boki AB i CD są równoległe. Oznacza to, że kąt BDC także ma miarę β. Trójkąt BCD jest trójkątem równoramiennym, gdyż podstawa CD ma mieć taką samą długość jak ramię BC. Boki BC i CD tworzą ramiona tego trójkąta równoramiennego, zaś przekątna BD to podstawa tego trójkąta. Oba kąty między ramieniem a podstawą trójkąta równoramiennego są sobie równe, a w tym przypadku tymi kątami są kąty DBC oraz BDC. Ich miary wynoszą odpowiednio α i β, co oznacza, że α = β. Co należało dowieść.

Zadanie 16.
89Zadanie 17.
90Zadanie 18.
90Zadanie 25.
98Zadanie 27.
98Zadanie 16.
103Zadanie 17.
103Zadanie 19.
103Zadanie 14.
111Zadanie 13.
114Zadanie 14.
114Zadanie 21.
131Zadanie 23.
137Zadanie 28.
138Zadanie 20.
142Zadanie 23.
148
