W tym zadaniu musisz zapisać jakim równaniem opisany jest okrąg, którego średnicę stanowi odcinek AB, gdzie A jest punktem o współrzędnych (-2, -2) zaś B = (4, 2).
Środek tego okręgu to środek średnicy, czyli odcinka AB.
![]()
Z kolei promień okręgu to połowa średnicy, czyli długości odcinka AB.
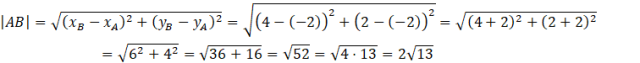
![]()
A więc szukane równanie okręgu ma postać:
![]()
![]()

Aby zapisać równanie okręgu potrzebujesz znać współrzędne środka tego okręgu oraz jego promień. Środek okręgu to także środek odcinka będącego średnicą. Więc aby wyznaczyć współrzędne środka tego okręgu musisz wyznaczyć środek odcinka AB, korzystając ze wzoru na środek odcinka.
![]()
Z kolei promień okręgu to połowa średnicy. Więc aby obliczyć promień tego okręgu musisz obliczyć długość odcinka AB, a następnie podzielić ją przez 2.
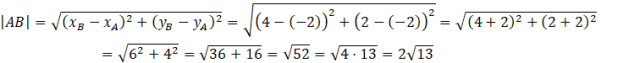
![]()
Podstawiając współrzędne środka okręgu oraz jego promień do równania okręgu otrzymasz końcowy rezultat.
![]()
![]()

Ćwiczenie B.
11Ćwiczenie C.
12Zadanie 1.
14Zadanie 2.
14Zadanie 6.
14Zadanie 9.
15Zadanie 10.
15Zadanie 12.
15Zadanie 13.
15Zadanie 14.
15Zadanie 16.
15Zadanie 17.
15Ćwiczenie A.
17Ćwiczenie B.
17Przykład 2.
19Zadanie 1.
20Zadanie 2.
20Zadanie 4.
20Zadanie 5.
20Zadanie 7.
20Zadanie 8.
20Zadanie 9.
21Zadanie 10.
21Zadanie 11.
21Zadanie 14.
21Zadanie 15.
21Zadanie 16.
21Zadanie 17.
22Zadanie 1.
26Zadanie 3.
26Zadanie 4.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 9.
27Zadanie 12.
27Ćwiczenie B.
29Zadanie 1.
30Zadanie 3.
30Zadanie 4.
30Zadanie 5.
30Zadanie 6.
30Zadanie 8.
31Zadanie 10.
31Zadanie 11.
31Zadanie 1.
35Zadanie 2.
35Zadanie 4.
36Zadanie 5.
36Zadanie 6.
36Zadanie 7.
36Zadanie 8.
36Zadanie 11.
36Zadanie 12.
36Zadanie 14.
37Zadanie 1.
38Zadanie 11.
38Zadanie 12.
38
