W tym zadaniu musisz wykazać, że prosta l zadana równaniem 2x – 4y + 1 = 0 oraz prosta k wyznaczana przez równanie x – 2y – 1 = 0 są do siebie równoległe oraz wyznaczyć jak odległe są od siebie te dwie proste.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
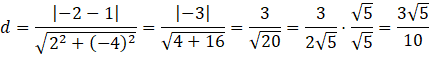

Dwie proste są do siebie równoległe, gdy ich współczynniki kierunkowe są takie same. Jednak równania podanych prostych są w postaci ogólnej, więc musisz zamienić tę postać, na postać kierunkową, aby odczytać współczynniki kierunkowe.
Spójrz, jak wygląda postać kierunkowa równania prostej. Po jednej stronie równania jest zawsze y, zaś po drugiej wyrażenie z x i wyraz wolny. Oczywiście współczynnik stojący przy x może wynosić 0, wtedy nie zapisuje się go i po drugiej stronie stoi jedynie wyraz wolny. Więc aby zapisać równanie w postaci kierunkowej musisz przenieść y na jedną stronę tak by był jedynym wyrażeniem z tej strony, a następnie ewentualnie pozbyć się liczby stojącej przy y.
![]()
![]()
![]()
Odczytaj współczynniki kierunkowy prostej l:
![]()
Podobnie postąp dla prostej k.
![]()
![]()
![]()
Odczytaj współczynnik kierunkowy prostej k:
![]()
Oba współczynniki kierunkowe są sobie równe, więc proste te są do siebie równoległe.
Aby obliczyć odległość prostych równoległych od siebie, skorzystaj ze wzoru:
![]()
Wzór jest dla prostych zadanych równaniami Ax + By + C1 = 0 oraz Ax + By + C2 = 0. Zauważ, że w obu równaniach współczynniki A i B wynoszą tyle samo. Więc musisz któreś równanie przemnożyć obustronnie przez pewną wartość, tak aby otrzymać dwa równania z tymi samymi współczynnikami A i B. Lepiej przemnożyć równanie prostej k przez 2, aby uniknąć ułamków.
![]()
![]()
Oczywiście, to jest ciągle równanie tej samej prostej. Teraz wystarczy, że odczytasz poszczególne współczynniki z obu równań, i podstawisz je do wzoru. A wynosi 2, B wynosi -4, C1 = 1, zaś C2 = -2.

Oczywiście, ponieważ w mianowniku pojawił się pierwiastek, musisz usunąć niewymierność z mianownika, przez przemnożenie zarówno licznika jak i mianownika przez ten pierwiastek.

Ćwiczenie B.
11Ćwiczenie C.
12Zadanie 1.
14Zadanie 2.
14Zadanie 6.
14Zadanie 9.
15Zadanie 10.
15Zadanie 12.
15Zadanie 13.
15Zadanie 14.
15Zadanie 16.
15Zadanie 17.
15Ćwiczenie A.
17Ćwiczenie B.
17Przykład 2.
19Zadanie 1.
20Zadanie 2.
20Zadanie 4.
20Zadanie 5.
20Zadanie 7.
20Zadanie 8.
20Zadanie 9.
21Zadanie 10.
21Zadanie 11.
21Zadanie 14.
21Zadanie 15.
21Zadanie 16.
21Zadanie 17.
22Zadanie 1.
26Zadanie 3.
26Zadanie 4.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 9.
27Zadanie 12.
27Ćwiczenie B.
29Zadanie 1.
30Zadanie 3.
30Zadanie 4.
30Zadanie 5.
30Zadanie 6.
30Zadanie 8.
31Zadanie 10.
31Zadanie 11.
31Zadanie 1.
35Zadanie 2.
35Zadanie 4.
36Zadanie 5.
36Zadanie 6.
36Zadanie 7.
36Zadanie 8.
36Zadanie 11.
36Zadanie 12.
36Zadanie 14.
37Zadanie 1.
38Zadanie 11.
38Zadanie 12.
38
