W tym zadaniu trzeba określić ilość rozwiązań układu równań wykorzystując jego interpretację geometryczną.
![]()
![]()
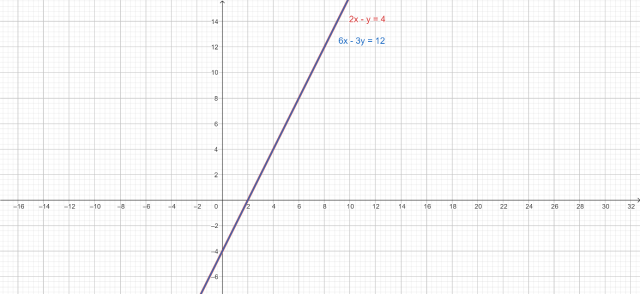
Proste opisane równaniami z układu równań pokrywają się, a więc ten układ równań ma nieskończenie wiele rozwiązań.

Aby określić, ile rozwiązań ma podany układ równań, przy użyciu jego interpretacji geometrycznej, musisz narysować wykresy równań które składają się na ten układ równań, a następnie odczytać w ilu punktach te równania się przecinają.
Do narysowania prostej potrzebujesz dwóch punktów. Najłatwiej je wyznaczyć podstawiając pewne łatwe w liczeniu liczby za x do równań.
Z pierwszego równania otrzymasz:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Więc prosta opisana przez pierwsze równanie będzie przechodzić przez punkty (0, -4) oraz (1, -2)
Z drugiego równania otrzymasz:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Więc prosta opisana przez drugie równanie będzie przechodzić przez punkty (0, -4) oraz (1, -2)
Następnie zaznacz te punkty w układzie współrzędnych i przeprowadź przez nie proste opisywane przez podane równania.

Ćwiczenie B.
11Ćwiczenie C.
12Zadanie 1.
14Zadanie 2.
14Zadanie 6.
14Zadanie 9.
15Zadanie 10.
15Zadanie 12.
15Zadanie 13.
15Zadanie 14.
15Zadanie 16.
15Zadanie 17.
15Ćwiczenie A.
17Ćwiczenie B.
17Przykład 2.
19Zadanie 1.
20Zadanie 2.
20Zadanie 4.
20Zadanie 5.
20Zadanie 7.
20Zadanie 8.
20Zadanie 9.
21Zadanie 10.
21Zadanie 11.
21Zadanie 14.
21Zadanie 15.
21Zadanie 16.
21Zadanie 17.
22Zadanie 1.
26Zadanie 3.
26Zadanie 4.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 9.
27Zadanie 12.
27Ćwiczenie B.
29Zadanie 1.
30Zadanie 3.
30Zadanie 4.
30Zadanie 5.
30Zadanie 6.
30Zadanie 8.
31Zadanie 10.
31Zadanie 11.
31Zadanie 1.
35Zadanie 2.
35Zadanie 4.
36Zadanie 5.
36Zadanie 6.
36Zadanie 7.
36Zadanie 8.
36Zadanie 11.
36Zadanie 12.
36Zadanie 14.
37Zadanie 1.
38Zadanie 11.
38Zadanie 12.
38
