W tym zadaniu musisz wyznaczyć jak długi jest promień okręgu o środku w punkcie S = (2, 3), jeśli cięciwa tego okręgu o długości 4 jest zawarta w prostej o równaniu $\text{[math]}$ .

Punkty przecięcia się podanej prostej, z okręgiem są odległe od środka okręgu o szukany promień. Z kolei odcinek prostopadły do podanej prostej, łączący środek okręgu z prostą, dzieli cięciwę dokładnie na dwie równe części, a długość tego odcinka to odległość środka okręgu od prostej.

Wobec tego: połowa cięciwy, odcinek prostopadły łączący środek okręgu z prostą oraz promień okręgu tworzą trójkąt prostokątny, którego przeciwprostokątną jest szukany promień.

$\text{[math]}$

Odległość środka okręgu od prostej:

$\text{[math]}$

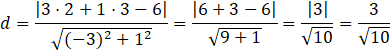
Połowa cięciwy = 2

$\text{[math]}$

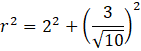
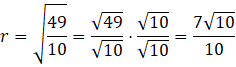
Zauważ, że punkty przecięcia się podanej prostej, z okręgiem są odległe od środka okręgu o szukany promień. Z kolei odcinek prostopadły do podanej prostej, łączący środek okręgu z prostą, dzieli cięciwę dokładnie na dwie równe części, a długość tego odcinka to odległość środka okręgu od prostej.

Wobec tego: połowa cięciwy, odcinek prostopadły łączący środek okręgu z prostą oraz promień okręgu tworzą trójkąt prostokątny, którego przeciwprostokątną jest szukany promień. Długość tego promienia możesz wyliczyć z twierdzenia Pitagorasa.

Jednakże wcześniej musisz znać długości dwóch przyprostokątnych tego trójkąta. Jedną z nich możesz podać od razu – jest to połowa długości cięciwy, czyli po prostu 2. Drugą z kolei musisz obliczyć ze wzoru na odległość punktu o współrzędnych (x₀, y₀) od prostej o równaniu Ax + By + C = 0. Wzór ten to:

$\text{[math]}$

Jednakże prosta która jest podana w zadaniu jest w postaci kierunkowej, więc musisz zamienić jej równanie na postać ogólną.

Spójrz, jak wygląda postać ogólna równania prostej. Po jednej stronie równania jest 0, zaś po drugie wyrażenia z x, y oraz wyraz wolny. Więc aby sprowadzić podane równania do postaci ogólnej musisz przenieść wszystkie składniki na jedną stronę. Dobrze jest także pozbyć się ewentualnych ułamków, przez przemnożenie obu stron przez ich mianowniki.

$\text{[math]}$

Teraz wystarczy, że odczytasz poszczególne współczynniki z równania, i podstawisz je do wzoru, razem z współrzędnymi punktu A.

$\text{[math]}$

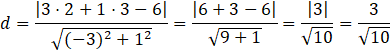
Przeważnie, gdy się pojawia niewymierność w mianowniku musisz ją usunąć. Jednakże, ponieważ będziesz wykorzystywał tę odległość w dalszych obliczeniach (a co więcej podnosił ją do kwadratu), to nie ma sensu usuwać tej niewymierności, gdyż w obecnej postaci łatwiej używać tej liczby w obliczeniach.

Korzystając z twierdzenia Pitagorasa, promień okręgu wynosi:

$\text{[math]}$

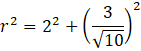
Ponieważ promień nie może być liczbą ujemną, to nie musisz pisać ujemnego rozwiązania.

$\text{[math]}$

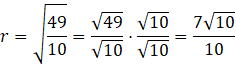
Oczywiście, ponieważ w mianowniku pojawił się pierwiastek, musisz usunąć niewymierność z mianownika, przez przemnożenie zarówno licznika jak i mianownika przez ten pierwiastek.