W tym zadaniu trzeba wyliczyć jaką długość ma cięciwa okręgu, którego środek ma współrzędne (2, -1) a jego promień wynosi 3 i która zawarta jest w prostej zadanej równanej 2y – x + 1 = 0.
Równanie rozważanego okręgu to:
![]()
![]()
Wyznaczanie punktów przecięcia się prostej z okręgiem:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Więc punkty przecięcia rozważanej prostej i okręgu to:
![]()
![]()
Szukana długość cięciwy to po prostu odległość między tymi dwoma punktami:
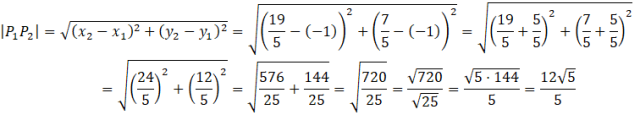

Aby wyznaczyć długość szukanej cięciwy najpierw musisz wyznaczyć punkty przecięcia się prostej zawierającej tę cięciwę z okręgiem, a następnie wyliczyć odległość między tymi punktami.
Współrzędne punktów przecięcia podanej prostej z okręgiem będą spełniać układ równań składający się z równań podanej prostej i okręgu. Mają być to punkty, które jednocześnie należą do tej prostej i okręgu, więc muszą spełniać równania je opisujące na raz.
Jednakże najpierw musisz wyznaczyć równanie tego okręgu. Podstaw współrzędne środka tego okręgu oraz jego promień do równania.
![]()
![]()
![]()
Z pierwszego równania musisz wyznaczyć x lub y w zależności od drugiej zmiennej. Łatwiej będzie wyznaczyć x w zależności od y. Wystarczy, że przeniesiesz x na drugą stronę.
![]()
Aby uzyskać równanie z jedną zmienną wystarczy, że do równania okręgu za x podstawisz wyrażenie z x.
![]()
![]()
Aby rozpisać nawiasy użyjesz wzoru skróconego mnożenia.
![]()
A następnie uprość wyrażenie i przenieś wszystkie składniki na jedną stronę.
![]()
Otrzymałeś równanie kwadratowe, które musisz rozwiązać przy użyciu Δ.
![]()
![]()
![]()
![]()
Teraz aby otrzymać pierwsze współrzędne tych punktów musisz podstawić otrzymane liczby do któregokolwiek równania. Oczywiście łatwiej jest wyliczyć x z wcześniej uzyskanej zależności.
![]()
![]()
Więc punkty przecięcia rozważanej prostej i okręgu to:
![]()
![]()
Szukana długość cięciwy to po prostu odległość między tymi dwoma punktami:
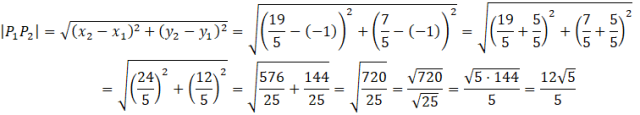

Ćwiczenie B.
11Ćwiczenie C.
12Zadanie 1.
14Zadanie 2.
14Zadanie 6.
14Zadanie 9.
15Zadanie 10.
15Zadanie 12.
15Zadanie 13.
15Zadanie 14.
15Zadanie 16.
15Zadanie 17.
15Ćwiczenie A.
17Ćwiczenie B.
17Przykład 2.
19Zadanie 1.
20Zadanie 2.
20Zadanie 4.
20Zadanie 5.
20Zadanie 7.
20Zadanie 8.
20Zadanie 9.
21Zadanie 10.
21Zadanie 11.
21Zadanie 14.
21Zadanie 15.
21Zadanie 16.
21Zadanie 17.
22Zadanie 1.
26Zadanie 3.
26Zadanie 4.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 9.
27Zadanie 12.
27Ćwiczenie B.
29Zadanie 1.
30Zadanie 3.
30Zadanie 4.
30Zadanie 5.
30Zadanie 6.
30Zadanie 8.
31Zadanie 10.
31Zadanie 11.
31Zadanie 1.
35Zadanie 2.
35Zadanie 4.
36Zadanie 5.
36Zadanie 6.
36Zadanie 7.
36Zadanie 8.
36Zadanie 11.
36Zadanie 12.
36Zadanie 14.
37Zadanie 1.
38Zadanie 11.
38Zadanie 12.
38
