![]()
![]()
![]()
![]()
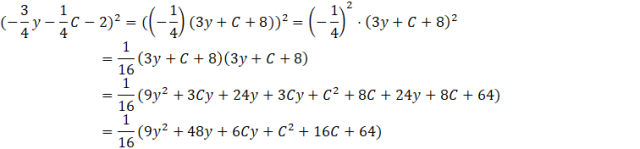
![]()
![]()
![]()
![]()
Ponieważ prosta styczna do okręgu ma tylko jeden punkt wspólny z tym okręgiem, więc powyższe równanie musi mieć jedno rozwiązanie. Ponieważ jest to równanie kwadratowe, to jedno rozwiązanie ma wtedy i tylko wtedy, gdy:
![]()
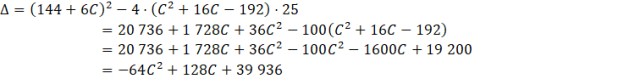
![]()
![]()
![]()
![]()
![]()
![]()
Rozważana prosta jest styczna do okręgu dla ![]()
Ponieważ dla otrzymanych wartości C, równanie kwadratowe zmiennej y z parametrem C, ma jedno rozwiązanie, to rozwiązanie to dane jest wzorem:
![]()
Dla C = 26
![]()
![]()
![]()
Więc punkt styczności dla C = 26 to:
![]()
Dla C = -24
![]()
![]()
![]()
Więc punkt styczności dla C = -24 to:
![]()

Punkt styczności będzie należał zarówno do szukanej prostej, jak i do podanego okręgu. Więc jego współrzędne będą spełniań oba równania na raz. Jednakże, równanie takie musi mieć jedno rozwiązane, gdyż dla jednej prostej stycznej do okręgu, jest tylko jeden punkt, który należy do obu. Gdyby były dwa takie punkty, to prosta przecinałaby okrąg, a nie byłaby styczna. Zapisz oba równania jako układ równań:
![]()
Aby rozwiązać ten układ równań musisz pierwsze równanie tak przekształcić, by uzyskać zależność x lub y od pozostałych zmiennych. Możesz wybrać, czy wyznaczysz to ze względu na x, czy y. Tutaj wybrane zostanie przekształcenie ze względu na x.
Przenieś wyrażenie z x na drugą stronę:
![]()
![]()
Teraz podstaw za x do równania okręgu.
![]()
Pierwszy nawias zawierający trzy składniki jest podniesiony do kwadratu. Rozpisz go sobie osobno jako iloczyn dwóch nawiasów i go przemnóż (możesz także skorzystać ze wzoru na kwadrat sumy trzech składników, jednakże w podstawie programowej nie ma tego wzoru). Mnożąc dwa nawiasy przez siebie, mnożysz każdy składnik ze sobą i je do siebie dodajesz. Warto uprościć otrzymane wyrażenie. Dla uproszczenia obliczeń, przed mnożeniem nawiasów wyciągnij ![]()
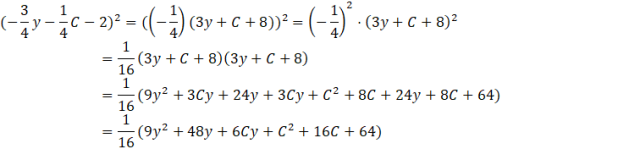
Wyrażenie z drugiego nawiasu oblicz przy użyciu wzoru skróconego mnożenia.
![]()
Przemnóż obie strony przez wspólny mianownik (16) aby pozbyć się ułamków
![]()
A następnie uprość wyrażenie i przenieś wszystkie składniki na jedną stronę. Warto także zapisać to jako równanie ze względu na y, a więc uporządkuj je tak, by wszystkie składniki z y były obok siebie.
![]()
Wyciągnij y z wyrazów które go zawierają.
![]()
Zauważ, że otrzymałeś równanie kwadratowe ze względu na y. Równanie to powinno mieć tylko jedno rozwiązanie (jedną wartość y będącą drugą współrzędną punktu styczności). Równanie kwadratowe ma jedno rozwiązanie tylko wtedy, gdy Δ = 0. Więc musisz obliczyć Δ i przyrównać ją do zera.
![]()
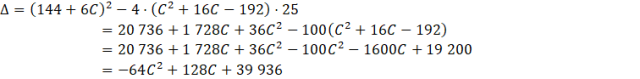
![]()
Zauważ, że każdy ze składników jest podzielny przez 64. Dla uproszczenia obliczeń warto podzielić obie strony przez 64.
![]()
Otrzymałeś kolejne równanie kwadratowe, które musisz rozwiązać przy użyciu Δ. Dla odróżnienia od poprzedniej Δ, dodaj do tej dodatkowy indeks.
![]()
![]()
![]()
![]()
Aby znaleźć współrzędne punktów styczności (czyli x oraz y) musisz podstawić otrzymane wartości C do układu równań i go rozwiązać. Jednak zauważ, że z wcześniejszych obliczeń masz już równanie kwadratowe z y oraz C, co więcej wiesz, że dla otrzymanych wartości C takie równanie ma jedno rozwiązanie. Jeśli równanie kwadratowe ma jedno rozwiązanie, to rozwiązanie to wyraża się wzorem:
![]()
Podstawiając wartości C otrzymasz szukane drugie współrzędne punktów styczności. Aby znaleźć pierwsze współrzędne (x) musisz wrócić do zależności między x, a y oraz C.
Dla C = 26
![]()
![]()
![]()
Więc punkt styczności dla C = 26 to:
![]()
Dla C = -24
![]()
![]()
![]()
Więc punkt styczności dla C = -24 to:
![]()