W tym zadaniu musisz wyznaczyć jakie współrzędne będzie miał punkt, który będzie symetryczny do punktu P o współrzędnych (2, 3) względem prostej zadanej równaniem ![]()
P’ – punkt symetryczny do punktu P względem prostej
k – prosta![]()
l – prosta prostopadła do prostej k
![]()
![]()
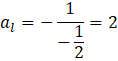
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Środek odcinka łączącego P i P’ to punkt przecięcia się prostych k i l.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Więc współrzędne punktu P’ wynoszą:
![]()

Szukany punkt (oznaczony jako P’) leży na prostej prostopadłej do prostej z zadania (niech prosta z zadania będzie prostą k, zaś prosta prostopadła do niej na której leży P’ będzie prostą l). Na prostej l leży także punkt P.
Zależność między współczynnikami kierunkowymi prostych k oraz l wygląda następująco:
![]()
Współczynnik kierunkowy prostej k możesz odczytać z jej równania i wynosi on ![]()
Współczynnik kierunkowy prostej l wynosi więc:

Pamiętaj, że dzieląc przez ułamek, mnożysz przez jego odwrotność.
Równanie prostej l możesz na chwilę obecną zapisać jako:
![]()
Prosta l przechodzi, przez punkt P, więc podstawiając do równania kierunkowego prostej l za x pierwszą współrzędną P, powinieneś otrzymać w wyniku drugą współrzędną.
![]()
![]()
![]()
Więc prosta l wyraża się wzorem:
![]()
Skoro punkt P’ leży na prostej l, to jego współrzędne możesz zapisać jako:
![]()
Punkt przecięcia się prostej l oraz k leży dokładnie pośrodku odcinka łączącego P oraz P’. Wyznacz najpierw ten punkt przecięcia, przez porównanie równań prostych k oraz l (gdyż obie proste osiągają w tym punkcie dokładnie tę samą wartość).
![]()
![]()
![]()
Aby wyznaczyć drugą współrzędną punktu przecięcia musisz podstawić otrzymaną pierwszą współrzędną, do któregokolwiek równania prostej.
![]()
![]()
Więc współrzędne punktu przecięcia się prostych k oraz l, a zarazem środek odcinka PP’ to:
![]()
Korzystając ze wzoru na środek odcinka możesz zapisać, że:
![]()
Porównując odpowiednie współrzędne do siebie oraz podstawiając odpowiednie współrzędne P, otrzymasz równania z których wyliczysz współrzędne punktu P’.
![]()
Oba równania możesz przemnożyć „na krzyż”.
![]()
![]()
![]()
![]()
Więc współrzędne punktu P’ wynoszą:
![]()

Ćwiczenie B.
11Ćwiczenie C.
12Zadanie 1.
14Zadanie 2.
14Zadanie 6.
14Zadanie 9.
15Zadanie 10.
15Zadanie 12.
15Zadanie 13.
15Zadanie 14.
15Zadanie 16.
15Zadanie 17.
15Ćwiczenie A.
17Ćwiczenie B.
17Przykład 2.
19Zadanie 1.
20Zadanie 2.
20Zadanie 4.
20Zadanie 5.
20Zadanie 7.
20Zadanie 8.
20Zadanie 9.
21Zadanie 10.
21Zadanie 11.
21Zadanie 14.
21Zadanie 15.
21Zadanie 16.
21Zadanie 17.
22Zadanie 1.
26Zadanie 3.
26Zadanie 4.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 9.
27Zadanie 12.
27Ćwiczenie B.
29Zadanie 1.
30Zadanie 3.
30Zadanie 4.
30Zadanie 5.
30Zadanie 6.
30Zadanie 8.
31Zadanie 10.
31Zadanie 11.
31Zadanie 1.
35Zadanie 2.
35Zadanie 4.
36Zadanie 5.
36Zadanie 6.
36Zadanie 7.
36Zadanie 8.
36Zadanie 11.
36Zadanie 12.
36Zadanie 14.
37Zadanie 1.
38Zadanie 11.
38Zadanie 12.
38
