W tym zadaniu musisz wyznaczyć równanie okręgu wpisanego w trójkąt przedstawiony na ilustracji obok, wiedząc, że trójkąt ten jest prostokątny i równoramienny.

Okrąg jest okręgiem wpisany w narysowany trójkąt, gdyż jest styczny do każdego boku tego trójkąta. Ponieważ jest to trójkąt prostokątny, to promień szukanego okręgu wyraża się wzorem:

$\text{[math]}$

Gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej.

Skoro trójkąt ten jest równoramienny, to długości jego przyprostokątnych są równe, czyli a = b.

$\text{[math]}$

Oś OY układu współrzędnych jest osią symetrii tego trójkąta (gdyż pokrywa się z wysokością opuszczoną na przeciwprostokątną, która w przypadku trójkąta równoramiennego dzieli ją na dwie, równe części), więc długość całej przyprostokątnej to dwukrotność długości odcinka między przecięciem tej osi z przeciwprostokątną, a wierzchołkiem trójkąta.

Na podstawie rysunku można stwierdzić, że połowa przeciwprostokątnej ma długość 1, czyli cała przeciwprostokątna ma długość 2.

$\text{[math]}$

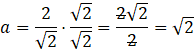
Środek szukanego okręgu leży na osi symetrii tego trójkąta, czyli osi OY. Wobec czego równanie tego okręgu przedstawia się następująco:

$\text{[math]}$

Gdzie y_S to współrzędna y środka szukanego okręgu.

Punkt (0, 0) należy do tego okręgu.

$\text{[math]}$

Więc równanie szukanego okręgu to:

$\text{[math]}$

Aby zapisać równanie szukanego okręgu musisz znać jego promień oraz współrzędne środka okręgu. Ponieważ okrąg ten jest wpisany w ten trójkąt (gdyż jest jednocześnie styczny do wszystkich jego boków), to jego promień możesz wyliczyć ze wzoru na długość promienia okręgu wpisanego w trójkąt prostokątny:

$\text{[math]}$

Gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej.

Skoro trójkąt ten jest równoramienny, to długości jego przyprostokątnych są równe, czyli a = b.

Zapisując twierdzenie Pitagorasa dla tego trójkąta otrzymasz:

$\text{[math]}$

Punkt przecięcia się osi OY z przeciwprostokątną, jak można odczytać z rysunku, to (0, 0), zaś jeden z wierzchołków tego trójkąta to (1, 0), co oznacza, że ten odcinek ma długość wynoszącą 1. Więc cała przeciwprostokątna tego trójkąta ma długość 2.

Podstawiając otrzymaną wartość do zależności między długością przyprostokątnej a przeciwprostokątnej otrzymasz długość pozostałych boków.

$\text{[math]}$

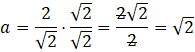
Oczywiście ponieważ, w mianowniku pojawił się pierwiastek, to musisz usunąć niewymierność z mianownika poprzez przemnożenie licznika i mianownika przez ten pierwiastek.

Mając długości wszystkich boków, możesz podstawić je do wzoru na promień okręgu wpisanego i wyliczyć go:

$\text{[math]}$

Zauważ, że okrąg, którego równania szukasz jest przedzielony osią symetrii dokładnie na dwie równe części. Więc jego środek leży na tej osi, czyli osi OY. Oznacza to, że pierwsza współrzędna środka tego okręgu wynosi 0. Wobec czego równanie tego okręgu przedstawia się następująco:

$\text{[math]}$

(Ze względu na kolizję oznaczeń druga współrzędna środka okręgu będzie tu nazywana jako y_S)

$\text{[math]}$

Zauważ, że punkt (0, 0) jest punktem, który należy do tego okręgu, więc podstawiając jego współrzędne do równania okręgu, za x oraz y otrzymasz prawdziwą zależność.

$\text{[math]}$

Pierwiastek z kwadratu pewnej liczby to wartość bezwzględna tej liczby. Promień tego okręgu jest oczywiście dodani, więc możesz pominąć wartość bezwzględną tej liczby. Z kolei na podstawie rysunku możesz stwierdzić, że y_S także jest dodatni (środek okręgu jest nad osią OX), więc minus przy y_S zamieni się na plus. Ostatecznie otrzymasz:

$\text{[math]}$